Қиылысқан түзулер
АВ және СD түзулері О нүктесінде қиылысып, бір-бірімен тік бұрыш жасасын (46-сурет). Сонда ∠ВОD = 90° болады. Ол жазық бұрыштың жартысы болғандықтан, ∠DОА = 90°, ∠СОВ = 90°. Бұдан ∠АОС = 90°-қа тең. Бұл жағдайда АВ және СD түзулері перпендикуляр болады.
А н ы қ т а м а. Тік бұрыш жасап қиылысқан екі түзу перпендикуляр түзулер (Лат. perpendicularis — тік сызык.) деп аталады.

Түзулердің перпендикулярлығы “⊥” таңбасымен белгіленеді. Мына а ⊥ b жазуы былай оқылады: “ а түзуі Ь түзуіне перпендикуляр”. Сонда “АВ түзуі СD түзуіне перпендикуляр” дегенді қысқаша АВ ⊥ СD деп жазамыз.
Перпендикуляр түзулерде жатқан кесінділер де, сәулелер де перпендикуляр болады, яғни 46-суреттегі ОВ және ОD сәулелері, сондай-ақ ОЕ, ОN кесінділері перпендикуляр.
Үшінші түзуге перпендикуляр екі түзудің қиылыспайтындығын көрсетелік.
Шындығында, АВ түзуіне перпендикуляр СС1 және DD1 түзулерін қарастыралық (47.1-сурет).
АВ түзуінің бойымен бүктедік делік, сонда суреттің үстіңгі бөлігі, астыңғы бөлікке түседі. 1 және 2 тік бұрыштар тең болғандықтан АС сәулесі АС1 сәулесімен беттеседі.
Осы сияқты ВD сәулесі ВD1 сәулесі-мен беттеседі. Сондықтан, егер СС1 мен DD1 түзулері Е нүктесінде қиылысады десек, онда бүл нүкте Е1 нүктесіне ауысып, осы түзулерде жатар еді де (47.2-сурет), біз Е, Е1 нүктелерінен өтетін СС1 мен DD1 түзулерін алар едік. Бұл мүмкін емес. Демек, біздің қиылысады деуіміз дұрыс емес, яғни СС1 және DD1 түзулері қиылыспайды.


Теорема 1
1-теорема. Тұзуден тысқары жатқан нүктеден осы түзуге перпендикуляр болатын тек бір ғана түзу жүргізуге болады.
Дәлелдеу. СD түзуі және ол түзуде жатпайтын В нүктесі берілсін (48.1-сурет). Алдымен В нүктесінен СD түзуіне перпендикуляр жүргізуге болатынын көрсетелік.
СD сәуледен ВСD бұрышына тең NСD бұрышын өлшеп саламыз (48.1-сурет). ВСD және NСD бұрыштары тең болғандықтан, біріншісін екіншісінің үстіне СВ мен СD қабырғалары СN, СD қабырғаларының үстіне дәл түсетіндей етіп бүктеуге болады. Бұл жағдайда В нүктесі СN сәулесінің қайсыбір В1 нүктесіне ауысады (48.2-сурет). СD мен ВВ1 түзулерінің қиылысу нүктесін А деп белгілейік. Сонда ВА кесіндісі СD түзуіне перпендикуляр болады. Шындығында, суретті бүктегенде АВ сәулесі АВ1 сәулесімен беттеседі, сондықтан бұрыш 1 мен бұрыш 2 дәл келеді. Демек, ∠1 = ∠2. 1 мен 2 іргелес бүрыштар болғандықтан, олардың әрқайсысы тік бұрыштар. Олай болса, ВА ⊥ СD.



Енді В нүктесінен СD түзуіне тек бір ғана перпендикуляр түзу жүргізуге болатынын дәлелдейік.
Егер В нүктесінен СD түзуіне тағы бір ВА1 перпендикуляр түзу жүргізуге болады десек, онда СD түзуіне перпендикуляр болатын ВА және ВА1 түзулері қиылысатын болып шығады (49-сурет).
Жоғарыда дәлелденгендей бұл мүмкін емес. Сонымен, В нүктесінен СD түзуіне перпендикуляр тек бір ғана түзу жүргізуге болады. Теорема дәлелденді.
Теорема 2
2-теорема. Түзудің әрбір нүктесі арқылы оған перпендикуляр тек бір ғана түзу жүргізуге болады.
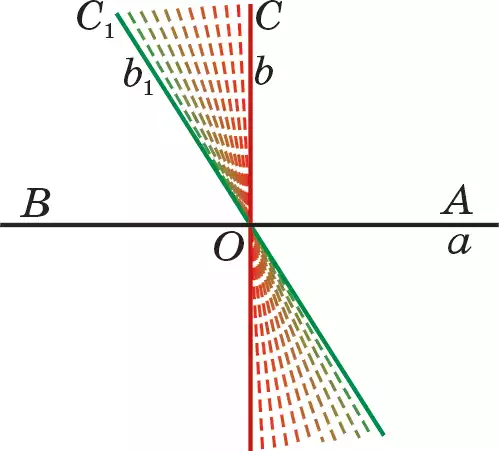
Дәлелдеу. Берілген а түзуінің бойынан (50-сурет) кез келген О нүктесін алайық. а түзуі аркылы анықталған жарты жазықтықтардың бірінде ОА сәулесінен бастап ∠АОС = 90° болатын бұрышты өлшеп салайық. Сонда ОС ⊥ ОА болады. ОС сәулесіне ОD толықтауыш сәулесін жүргізсек, b түзуі анықталады. Демек, b ⊥ а.
Енді О нүктесі арқылы өтетін және а түзуіне перпендикуляр бір ғана b түзуі болатынын көрсетейік. ОС сәулесі жатқан жарты жазықтықта ОС1 ⊥ ОА болатын тағы бір ОС1 сәулесі бар деп есептесек, ол b1 түзуін анықтайды. Сонда ∠АОС1 = 90°. Бірақ IV2 аксиомасы бойынша берілген жарты жазықтықта ОА сәулесінен бастап 90°-қа тең болатын бір ғана бұрышты өлшеп салуға болады. Демек, ОС1 сәулесі ОС сәулесіне немесе b1 түзуі b түзуіне дәл келеді.
Сонымен а түзуінің О нүктесі арқылы өтетін, оған перпендикуляр бір ғана b түзуі бар. Теорема дәлелденді.
В нүктесінен а түзуіне түсірілген ВА кесіндісін — перпендикуляр, ал ВС кесіндісін — көлбеу деп атайды (51-сурет). А нүктесі ВА перпендикулярының табаны, С нүктесі ВС көлбеуінің табаны, АС кесіндісі ВС көлбеуінің а түзуіндегі проекциясы деп аталады.
ВА кесіндісінің ұзындығын В нүктесінен а түзуіне дейінгі қашықтық деп те атайды.

Сұрақтар
1. Теоремаларды дәлелдеуде кандай аксиома, теоремалар пайдаланылды?
Жаттығулар
88. а түзуі берілген. Транспортирдің көмегімен а түзуіне перпендикуляр b түзуін жүргізіңдер.
89. а түзуі және одан тыс жатқан А нүктесі берілген. А нүктесі арқылы өтетін, а түзуіне перпендикуляр b түзуін жүргізіңдер. Үшбүрышты сызғышты пайдаланыңдар.
90. а және b түзулерінің қиылысуында пайда болған бұрыштардың үшеуі өзара тең. а ⊥ b екенін дәлелдеңдер.
91. Бір түзуге жүргізілген перпендикуляр және көлбеу түзулердің қиылысатынын дәлелдеңдер.
92. АВ және СD перпендикуляр түзулері О нүктесінде қиылысады. ОЕ және ОҒ сәулелері ОD сәулесімен бір жарты жазықтықта жатады және ∠ЕОF =105°, ∠ВОF = 28°. DОҒ және DОЕ бұрыштарын табыңдар.
93. Төбелері ортақ бір сүйір және бір доғал бұрыш берілген. Ол бұрыштардың сәйкес қабырғалары перпендикуляр. Пайда болған екі сүйір бұрыштың тең болатынын дәлелдеңдер.
94. Төбелері ортақ, сәйкес қабырғалары перпендикуляр екі бұрыш берілген. Олардың бірі екіншісінен 4 есе кем. Осы бүрыштарды табыңдар.
95. КМ мен LN түзулері О нүктесінде қиылысады және КМ ⊥ LN. ОК сәулесімен 58° бұрыш жасайтын ОD сәулесі жүргізілген. ОМ мен ОL сәулелерінің арасынан ∠РОМ + ∠LОD = 75° болатын етіп, ОР сәулесі жүргізілген. ОD, ОL, ОР сәулелері КМ түзуіне қарағанда бір жарты жазықтықта жатады. РОМ және LОР бұрыштарын табыңдар.