Определение
Как вам известно, две прямые на плоскости могут пересекаться, не пересекаться, совпадать.
Определение: Прямые, лежащие на одной плоскости, не имеющие общих точек, называются параллельными прямыми.
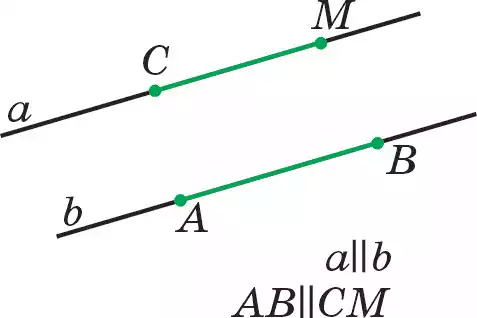
На рис. 76 даны параллельные прямые а и b. Для обозначения параллельности используется символ “ || ”. Запись а||b читается: “прямая а параллельна прямой b”. Отрезки и лучи, лежащие на параллельных прямых, также параллельны. На рис. 76 отрезки АВ и СМ, а также лучи АВ и СМ, лежащие на прямых а и b, параллельны: АВ || СМ.
Известно, что на плоскости через точку М проходит бесконечно много прямых. Тогда возникает вопрос: сколько можно провести прямых, проходящих через точку М и параллельных данной прямой b.
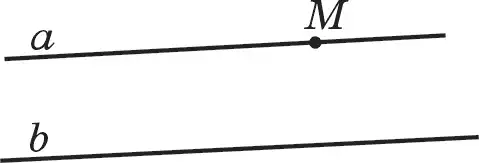
Пусть дана точка М (рис. 77). Для того чтобы начертить параллельные прямые, используется двусторонняя линейка. Если одну сторону линейки совместить с прямой, проходящей через точку М, и провести прямую по обе стороны линейки, то они будут параллельны: a || b.
Допустим, прямая b параллельна прямой а, проходящей через точку М. Другими словами, найдется прямая а, параллельная прямой b и проходящая через точку М, лежащую вне прямой b. На вышесказанный вопрос отвечает аксиома V.
V. Через точку, лежащую вне данной прямой на плоскости, можно провести одну и только одну прямую, параллельную данной прямой.
Это утверждение называется аксиомой параллельности. Она играет важную роль в доказательстве многих теорем. Таким образом, через точку М проходит только одна прямая а, параллельная данной прямой b (рис. 77).
Теорема
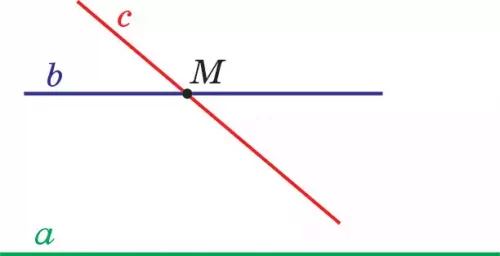
Теорема. Если какая-либо прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую.
Доказательство. Пусть даны прямые а и b такие, что а || b, и прямая с, пересекающая прямую в точке М (рис. 78).
Докажем, что прямая с пересекает и прямую а.
Предположим обратное, что прямая с не пересекает прямую а. Тогда выходит с || а. Получается, через точку М проходят две прямые b и с, параллельные прямой а. Это противоречит аксиоме V. Значит, прямые с и а не параллельные, а пересекаются. Теорема доказана.
В связи с доказательством этой теоремы обращаем ваше внимание на использованный метод доказательства. Его называют методом доказательства от противного. Доказательство теоремы по данному методу состоит из следующих этапов: 1) предположим противное, т. е. что заключение теоремы неверно;
2) исходя из этого предположения, проводим рассуждения; 3) в результате рассуждений приходим к ранее известным истинным утверждениям (аксиомам, доказанным теоремам), которые опровергают наше предположение; 4) на основании этого противоречия делаем вывод о верности заключения теоремы.
В жизни мы часто встречаемся с понятием параллельности. При строительстве зданий строго учитывается понятие параллельности.
Самый наглядный пример параллельности прямых-железнодорожное полотно. Еще одним примером применения понятия параллельных прямых является эскалатор. Все эти устройства помогают нам в повседневной жизни.
Вопросы
1. Можно ли утверждать, что если какая-либо прямая пересекает одну из трех параллельных прямых, то она пересекает и остальные? Ответ обоснуйте.
2. Распишите доказательство теоремы о параллельных прямых, пересеченных третьей прямой, по указанным этапам.
Упражнения
150. Даны прямая l и точка М, не лежащая на этой прямой. Через точку М: а) проведите прямые а, b, пересекающие прямую l; б) проведите прямую с, араллельную прямой l.
151. Приведите примеры параллельных прямых из окружающей среды.
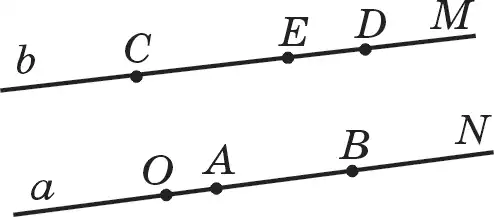
152. Даны параллельные прямые а || b (рис. 79). Отметьте на этих прямых отрезки АВ, СD, ЕD и учи ОN, СМ. Укажите параллельные отрезки и параллельные лучи. Почему они параллельны?
153. Верно ли утверждение, что, если а пересекает b и b пересекает с, то прямые а и с ересекаются?
154. Даны прямая а и точка А, не лежащая на этой прямой. Докажите, что хотя бы две прямые из трех, проходящих через точку А, пересекают прямую а.
155. Проведите прямую l, отметьте точки А, В, не лежащие на этой прямой. Через каждую из этих точек проведите прямую, параллельную прямой l. Как располагаются эти прямые?
156. Даны прямые а, b. Если а || b, то будет ли b || а? Объясните.
157. Прямые а и b пересекаются в одной точке. Существует ли прямая, параллельная каждой из них?
158. Даны прямые а, b, с, а || b, а прямые b и с пересекаются. Докажите, что пересекаются и прямые а и с .
159. Развернутый угол разделен лучом в отношении 1 : 4. Найдите градусные меры полученных углов.