Определения
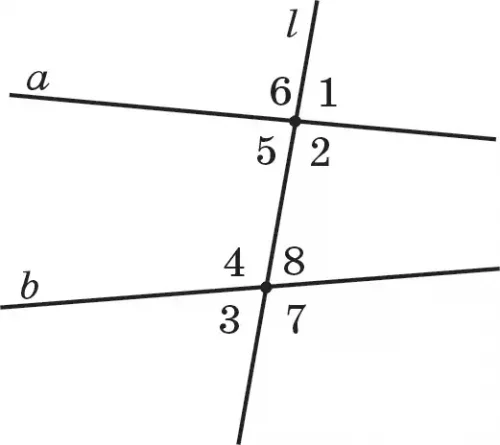
Пусть прямая l пересекается с прямыми а и b в точках А и В (рис. 80.1). При пересечении они образуют восемь углов. На рисунке углы обозначены цифрами. В этом случае прямую l называют секущей.
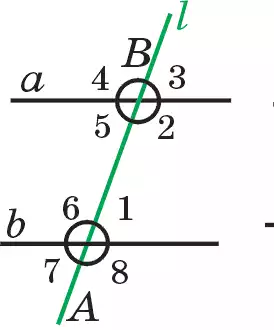
По расположению относительно секущей прямой углы имеют следующие названия: находящиеся между прямыми а и b и лежащие в разных полуплоскостях по отношению к прямой l ∠2 и ∠6, а также ∠1 и ∠5 называются внутренними накрест лежащими углами. Тогда ∠3 и ∠7, как и ∠4 и ∠8, образуют внешние накрест лежащие углы (рис. 80.1).
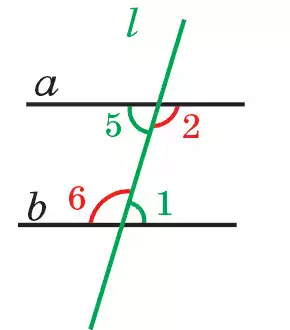
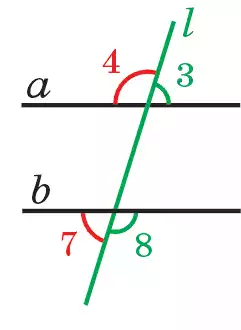
Находящиеся между прямыми а и b и лежащие в одной полуплоскости по отношению к секущей прямой l ∠1 и ∠2, ∠5 и ∠6 образуют внутренние односторонние углы (рис. 80.2), а ∠3 и ∠8, ∠4 и ∠7 — внешние односторонние углы (рис. 80.3). Два угла, один из которых находится между прямыми а и b, а второй — вне их, и лежащие в одной полуплоскости относительно секущей l, называются соответственными. ∠1 и ∠3, ∠6 и ∠4, ∠2 и ∠8, ∠5 и ∠7 будут соответственными углами (рис. 80.1).
Нижеследующие две теоремы раскрывают признаки параллельности прямых.
Теорема 1
Теорема 1. Если каждая из двух прямых параллельна третьей прямой, то они взаимно параллельны.
Доказательство. Пусть каждая из прямых а и b параллельна прямой с, т. е. а || с и b || с (рис. 81.1 ). Докажем, что а || b.
Допустим обратное, что прямые а и b не параллельны и пересекаются в какой-либо точке М (рис. 81.2). Тогда через точку М параллельно прямой с проходят две прямые а и b. Это противоречит аксиоме параллельности прямых (V). Таким образом, наше предположение неверно. Значит, а || b. Теорема доказана.


Теорема 2
Теорема 2. Если внутренние накрест лежащие углы, образованные двумя прямыми и секущей, равны, то эти две прямые параллельны.
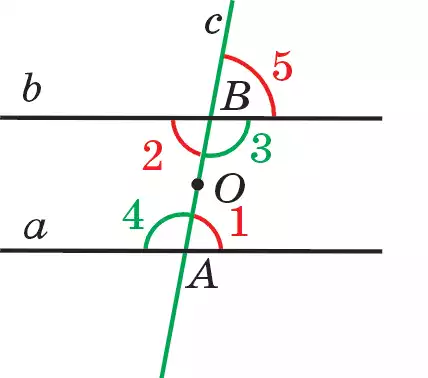
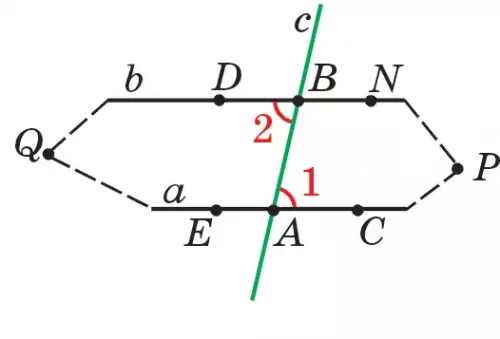
Доказательство. Пусть прямая с пересекает прямые а, b соответственно в точках А и В (рис. 82.1 ). Докажем, что если внутренние накрест лежащие углы ∠1 и ∠2 равны, то прямые а и b параллельны. Обозначим середину отрезка АВ через точку О. Допустим, что прямые а и b не параллельны, а пересекаются в точке Р (рис. 82.2). Известно, что равные фигуры можно совместить друг с другом. Так как ∠1 = ∠2 и ОА = ОВ, их можно совместить, наложив друг на
друга. Если с этой целью прямые а, b, с в точке О повернуть на 180° , т. е. симметрично отражать относительно центра О, тогда точки А и В, лучи ОА и ОВ, АС и ВD, АЕ и ВN, а также прямые а и b поменяются местами (рис. 82.2). Тогда точка Р, лежащая на пересечении лучей АС и ВN, переходит в точку Q, лежащую на пересечении лучей ВD (АС) и АЕ (ВN). В итоге прямые а и b пересекаются в двух точках Р, Q, т. е. получается, что через две точки Р, Q проходят две различные прямые а и b. Это противоречит основному свойству I2. Поэтому прямые а и b не пересекаются, они будут параллельными. Теорема доказана.
Ясно, что теорема верна и для внутренних накрест лежащих углов ∠3 и ∠4, так как, если ∠1= ∠2, то ∠3 = ∠4. В самом деле ∠1 + ∠3 =180°, ∠2 + ∠4 = 180°. Откуда ∠3 = ∠180° – ∠1, ∠4 = ∠180° – ∠2.
В последних двух равенствах равны их правые части, а следовательно будут равными и их левые части, т. е. ∠3 = ∠4.
Теорема 3
Теорема 3. Если при пересечении двух прямых третьей: а) сумма внутренних односторонних углов равна 180°; б) соответственные углы равны, то данные две прямые параллельны. Эта теорема легко доказывается на основе предыдущей теоремы.
Доказательство. а) Докажем теорему для внутренних односторонних углов ∠1 и ∠4 (рис. 82.1). По условию теоремы ∠2 + ∠4 = 180°, но ∠1 + ∠4=180°.
Из этих двух равенств следует, что ∠1 = ∠2. В этом случае имеет место предыдущая теорема. Значит, при наличии равенства ∠2 + ∠4 = 180°
выполняется а || b. б) Докажем это для соответственных углов ∠1 и ∠5. По условию теоремы ∠1 = ∠5. Так как углы вертикальные, то ∠2 = ∠5.
Из последних двух равенств следует, что ∠1 = ∠2. На основе предыдущей теоремы а || b. Теорема доказана.
Вопросы
1. Если прямая параллельна каждой из данных прямых, то какими будут данные прямые?
2. Знание каких аксиом и теорем было применено при доказательстве теорем?
Упражнения
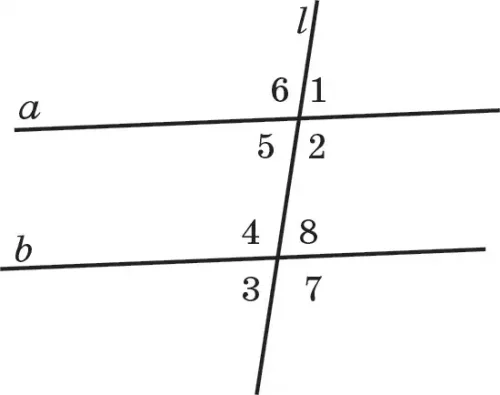
160. При пересечении прямой l с любыми прямыми а и b образуются 8 углов (рис. 83). Они обозначены цифрами. 1) Даны ∠2 = 95°, ∠4=100°. Найдите ∠5 и ∠8. 2) Известно, что ∠2 + ∠8 = 160°. Найдите сумму ∠5 + ∠4. 3) Известно, что ∠4 – ∠5 = 15°. Найдите разность ∠2 – ∠8.
161. Прямые а и b параллельны, а прямая l пересекает их (рис.84). Относительно полученных углов при пересечении докажите нижеследующее: 1) ∠1 = ∠3; 2) ∠1= ∠8; 3) ∠6 =∠7; 4) ∠7+ ∠1=180°.
162. Один из углов, образовавшихся при пересечении двух параллельных прямых третьей прямой, равен 65°. Найдите остальные углы.
163. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 40°. Найдите все эти углы, образованные при пересечении прямых.
164. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 160°.Чему равны эти углы, образованные при пересечении прямых.
165. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°.Чему равны углы, образованные при пересечении прямых?
166. Две параллельные прямые пересечены третьей прямой так, что один из образовавшихся углов равен 120°. Под какими углами его биссектриса пересекает вторую параллельную прямую?
167. Прямые АВ и СD пересечены третьей прямой МN в точках К и Z так, что точки А и С находятся в одной полуплоскости, аВ и D — в другой относительно прямой МN. ∠МКD = ∠МLВ. Докажите, что прямые АВ и СD параллельны.
168. Две параллельные прямые пересечены секущей. Докажите, что: 1) биссектрисы накрест лежащих углов параллельны; 2) биссектрисы соответственных углов параллельны; 3) биссектрисы односторонних углов перпендикулярны.