Теорема 1
Рассмотрим теоремы, обратные теоремам из «Признаки параллельности прямых«.
Теорема 1 (обратная теореме 2). Если две параллельные прямые пересекаются третьей, то внутренние накрест лежащие углы равны.
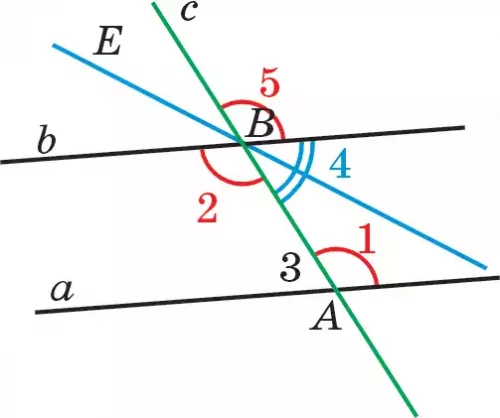
Доказательство. Пусть даны прямые а || b (рис. 85). Пусть ∠1 и ∠2 — внутренние накрест лежащие углы при пересечении этих прямых с прямой с.
Докажем, что ∠1 = ∠2. Допустим противоположное, пусть ∠1 ≠ ∠2. В этом случае на полуплоскости, определенной относительно прямой а, содержащей луч ВD, найдется такой луч ВЕ, чтобы выполнялось равенство ∠1=∠АВЕ.
Тогда на основании теоремы 2 из «Признаки параллельности прямых» получится, что ВЕ || а. В результате через точку В будут проходить две прямые b и ВЕ, параллельные прямой а. Это противоречит аксиоме V. Поэтому ∠1 = ∠2. Теорема доказана.
Теорема 2
Теорема 2 (обратная теореме 3). Если две параллельные прямые пересечены третьей, то: а) сумма внутренних односторонних углов равна
180°; б) соответственные углы равны.
Доказательство этой теоремы вытекает из теоремы 1. Оба утверждения теоремы 2 попробуйте доказать самостоятельно.
Если даны два угла, то их соответствующие стороны могут быть расположены по-разному. Рассмотрим случай, когда они параллельны. Вместе с тем соответствующие параллельные стороны могут иметь одинаковые или противоположные направления. Это зависит от направления лучей, которые образуют углы.
Теорема 3
Теорема 3. Если соответствующие стороны двух углов параллельны, то они либо равны, либо их сумма составляет 180°.
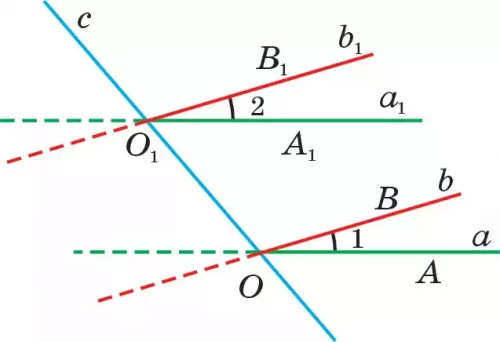
Доказательство. Пусть даны ∠1 и ∠2, а также соответствующие их стороны: а || а1, b || b1 (рис. 86).
Точки О и О1 являются вершинами углов. Пары углов ∠1, ∠2 или ∠1, ∠5 будут углами, удовлетворяющими условию теоремы. Через точки О и О1 проведем прямую с.
1) Рассмотрим ∠1 и ∠2. Пусть лучи ОА || О1А1 и ОВ || О1В1 одинаково направлены (рис. 86.1 ). На основании теоремы 2 имеем: ∠3 = ∠4
и ∠1 + ∠3 = ∠2 + ∠4, отсюда ∠1 = ∠2. Первая часть теоремы доказана.
2) Рассмотрим ∠1 и ∠5. Пусть ОА||О1А1 и OB||O1B1, при этом лучи ОВ и О1В1 сонаправлены, а лучи ОА и О1А1 противоположно направлены. Углы 5 и 2 являются смежными, отсюда ∠ 5 + ∠2 = 180°. Рис.86.2. А так как ∠2 = ∠1, то ∠1 + ∠5 = 180°.
Теорема доказана.

Следствие
Следствие. Два угла, соответствующие стороны которых одинаково или противоположно направлены, равны.
Вопросы
1. В чем сходство и различия между признаками и свойствами параллельных прямых?
2. Какие знания применены при доказательстве теорем?
Упражнения
169. Параллельные прямые а и b пересекаются с прямой с. Один из внутренних углов равен 107°. Под каким углом пересекает биссектриса данного угла вторую прямую?
170. Сумма одного из внутренних углов и угла, вертикального с ним, равна 240°. Найдите угол, соответственный с данным углом.
171. Прямая с пересекает прямую АВ в точке Е, а прямую СD в точке F. Если: 1) ∠АЕF = 90° и ∠ВЕD = 90°; 2) В и D лежат по одну сторону от прямой с и ∠ВЕF = 86°47′. ∠ЕFD = 93°13′, то будут ли параллельными прямые АВ и СD?
172. На рис. 84, если: 1) ∠6 = 92°; 2) ∠2 = 30°, то как изменить ∠8, чтобы прямые а и b были параллельными.
173. При пересечении двух параллельных прямых секущей разность образовавшихся внутренних односторонних углов равна 40°. Найдите эти углы.
174. Даны два угла АВС = 75° и ВСD =125°. Могут ли соответствующие стороны этих углов ВА и СD быть параллельными?
175. Докажите равенство двух углов, если их соответствующие стороны противоположно направлены, и каждый из них меньше развернутого.
176. АВС — прямой угол. Если ∠САВ = 43° и AD || ВC, то чему равен ∠DAC?
177. Отрезки АВ и СD пересекаются в точке О. Докажите, что АС || ВD, если АО = ОВ.
178. ∠АОВ = 52°. Через точку D, лежащую внутри ∠АОВ, проведены прямые, параллельные его сторонам. Найдите угол между этими прямыми и углы, образованные этими же прямыми и сторонами угла.
179. Даны два угла, стороны которых параллельны. Один из них больше второго на 70°. Найдите каждый угол.