Анықтама
Жазықтықтағы екі түзудін қиылысуы, қиылыспауы және беттесуі мүмкін екені белгілі.
А н ы қ т а м а. Бір жазықтықта жатқан және ортақ нүктесі болмайтын түзулер параллель түзулер деп аталады.
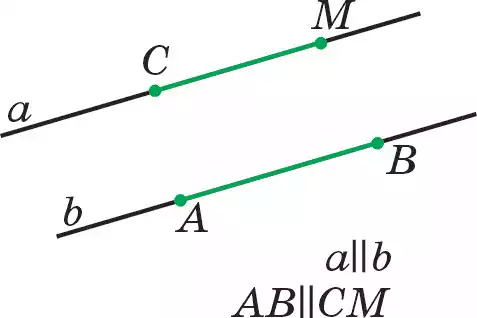
76-суретте бір-біріне параллель а және b түзулері кескінделген. Түзулердің параллельдігін белгілеу үшін “||” таңбасы пайдаланылады. а||b жазуы былай оқылады: “а түзуі b түзуіне параллель”. Параллель түзулерде жатқан кесінділер де, сәулелер де параллель деп есептеледі. 76-суреттегі а және b түзулерінде жатқан АВ мен СМ кесінділері де, сондай-ақ АВ мен СМ сәулелері де параллель болады: АВ || СМ.
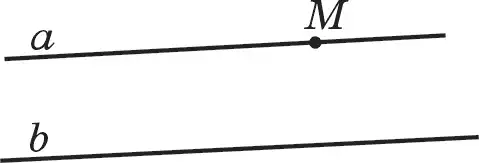
Жазықтықта М нүктесі арқылы шексіз көп түзулер жүргізуге болатыны белгілі. Сонда берілген М нүктесі арқылы өтетін және берілген b түзуіне параллель неше түзу жүргізуге болады? М нүктесі берілсін (77-сурет). Екі қырлы сызғыштың бір қырын М нүктесіне дәл келтіріп қойып, оның екі қыры арқылы а, b түзулерін сызайық, яғни а || b . М нүктесі арқылы өтетін түзуді а арқылы белгілейік. Демек, М нүктесі арқылы өтетін және қайсыбір b түзуіне параллель болатын а түзуі табылады. Жоғарыда қойылған сұраққа V аксиома жауап береді.
V. Жазықтықта берілген түзудің бойында жатпайтын нүкте арқылы берілген түзуге параллель тек бір ғана түзу өтеді.
Бұл сөйлем параллельдік аксиомасы деп аталды. Ол көптеген теоремаларды дәлелдеуде маңызды рөл атқарады.
Сонымен М нүктесі арқылы берілген b түзуіне параллель бір ғана а түзуі өтеді (77-сурет).
Теорема
Теорема. Егер қандай да бір түзу параллель екі түзудің біреуін қиып өтсе, онда ол екіншісін де қиып өтеді.
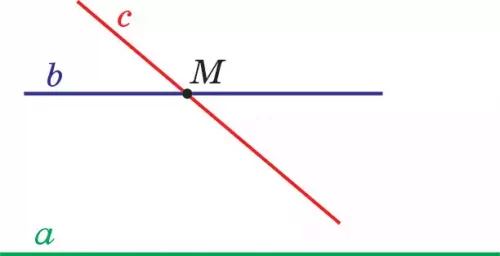
Дәлелдеу. а||b түзуі берілсін (78-сурет). с түзуі b түзуін М нүктесінде қиып өтсін. с түзуінің а түзуін де қиып өтетінін дәлелдейік.
Керісінше жорып, с түзуі а түзуімен қиылыспайды дейік. Сонда с || а болады да М нүктесі арқылы а түзуіне параллель b және с екі түзуі өтетін болып шығады. Бүл V аксиомаға қайшы. Олай болса, с және а түзулері қиылысады. Теорема дәлелденді.
Осы теореманың дәлелдемесіне байланысты дәлелдеу тәсіліне тоқталайық. Пайдаланылған әдісті теореманы дәлелдеудің кері жору әдісі дейміз.
Бұл әдіс бойынша теореманы дәлелдеу мынадай кезеңдерден тұрады:
1) теореманың қорытындысына кері жору жасаймыз, яғни қорытындыдағы пікір қате деп ұйғарамыз;
2) осы ұйғарымды талдаймыз;
3) талдай келе белгілі аксиомаға не дәлелденілген теоремаға қайшы келетін қорытындыға келеміз;
4) осы қайшылыққа сүйене отырып, кері жорудың дұрыс емес екенін дәлелдейміз.
Кері жорудың қателігі теореманың тура екенін дәлелдейді.
Біз күнделікті өмірде параллель ұғымымен жиі кездесеміз. Ғимараттардың құрылысы кезінде параллель ұғымы ескеріліп, қатаң сақталады. Параллель түзулерге бірден-бір мысал ретінде теміржол рельстерін атауға болады.
Сұрақтар
1. Егер кез келген түзу өзара параллель үш түзудің бірін қиятын болса, қалған түзулерді де қиып өтеді деген тұжырым ақиқат па?
2. Параллель түзулердің үшінші түзумен қиылысуы туралы теореманың дәлелдеуін аталған кезеңдерге бөліп, айтып беріңдер.
Жаттығулар
149. I түзуі және одан тыс М нүктесі берілген. М нүктесі арқылы 1) I түзуін қиып өтетін а, b түзулерін жүргізіңдер; 2) I түзуіне параллель с түзуін жүргізіңдер.
150. Қоршаған ортадан параллель түзулерге мысалдар келтіріңдер.
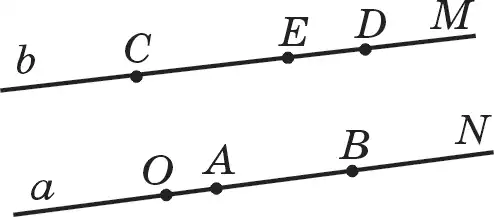
151. а мен b параллелъ түзулері берілген (79-сурет). Осы түзулердің бойынан АВ, СD, ЕD кесінділерін және ОN, СМ сәулелерін белгілеңдер. Параллель кесінділер мен параллель сәулелерді аныктаңдар. Параллель болу себебі неде?
152. Егер а мен b және b мен с түзулері қиылысса, а мен с түзулері қиылысады деп айтуға бола ма?
153. а түзуі мен осы түзуге тиісті емес А нүктесі берілген. А нүктесі арқылы өтетін үш түзудің ең болмаса екеуі а түзуін қиятынын дәлелдеңдер.
154. I түзуін жүргізіп, оған тиісті емес А, В нүктелерін белгілеңдер. Осы нүктелердің әрқайсысы арқылы I түзуіне параллель болатын түзу жүргізіңдер. Ол түзулер қалай орналасады?
155. а, b түзулері берілген. Егер а || b болса, b || а бола ма? Жауабын түсіндіріңдер.
156. а мен b түзулері бір нүктеде қиылысады. Олардың әрқайсысына параллель түзу бола ма? Жауабын түсіндіріңдер.
157. а, b, с түзулері берілген. а || b, ал b мен с қиылысады. а мен с түзулерінің де қиылысатынын дәлелдеңдер.
158. Сәуле жазыңқы бүрышты 1:4 қатынасында бөлсе, пайда болған бұрыштардың шамалары кандай?