Анықтамалар
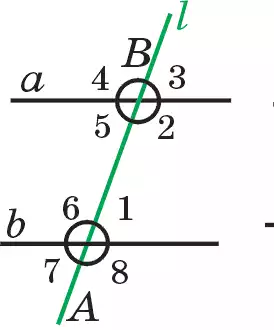
а және b түзулерін I түзуі А, В нүктелерінде қиып өтсін (80.1-сурет). Сонда олардың қиылысуьшан сегіз бұрыш пайда болады. Ол бұрыштар суретте цифрлармен көрсетілген. Бұл жағдайда I түзуін қиюшы деп атаймыз.
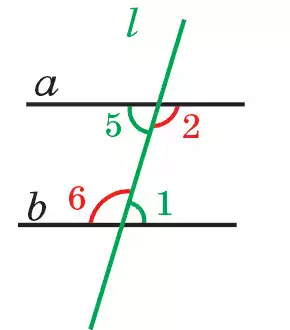
Ал бұрыштар үшін төмендегідей атау қабылданған. I түзуіне қарағанда әртүрлі жарты жазықта жатқан ∠2 мен ∠6 және ∠1 мен ∠5 ішкі айқыш бұрыштар деп аталады (80.2-сурет).
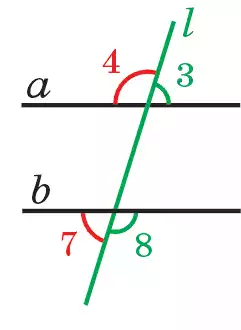
Ал 3- мен 7- және 4- мен 8-бұрыштар сыртқы айқыш бурыштар деп аталады (80.3-сурет).
I түзуіне қарағанда бір жарты жазықтықта жататын ∠1 мен ∠2 және ∠5 пен ∠6 — ішкі тұстас бұрыштар деп, ал ∠3 пен ∠8 және ∠4 пен ∠7 — сыртқы тұстас бұрыштар деп аталады (80.2-, 3-суреттер).
∠1 мен ∠3, ∠6 мен ∠4, ∠2 мен ∠8, ∠5 пен ∠7 сәйкес бұрыштар деп аталады (80.1-сурет).
Төмендегі екі теорема түзулердің параллельдігінің белгілерін мазмұңдайды.
1 Теорема
1-теорема. Егер екі түзудің әрқайсысы үшінші түзуге параллель болса, онда бұл екі түзу өзара параллель (Грек. рагаllеlоs — қатар жүруші) болады.
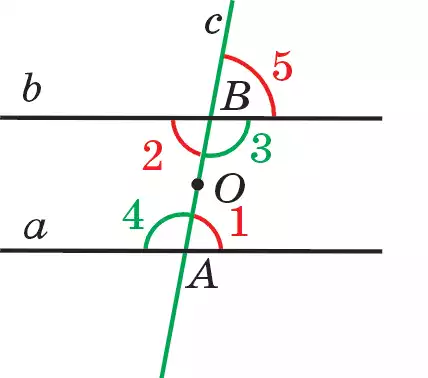
Дәлелдеу. а және b түзулерінің әрқайсысы с түзуіне параллель болсын (81.1-сурет). а 11 b екенін дәлелдейік.
Кері жорып, а және b түзулері параллель емес, олар қайсыбір М нүктесінде қиылысады дейік (81.2-сурет). Онда М нүктесі арқылы с түзуіне параллель екі түзу (а мен b) өтеді. Бүл параллельдік аксиомасына (V аксиомаға) қайшы. Сол себепті біздің кері үйғаруымыз дұрыс емес. Демек, а || b болады. Теорема дәлелденді.


2 Теорема
2-теорема. Егер екі түзу мен қиюшы жасайтын ішкі айқыш бұрыштар тең болса, онда бұл түзулер параллель болады.
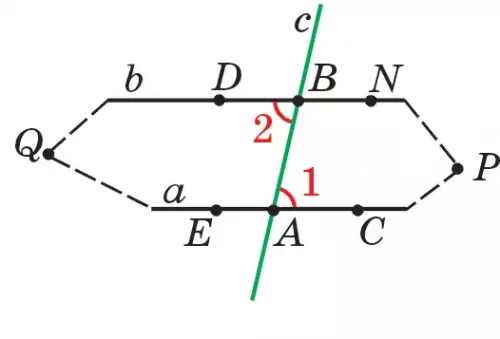
Дәлелдеу. а, b түзулерін с түзуі сәйкесінше А,В нүктелерінде қиып өтсін (82.1-сурет).
Егер ∠1, ∠2 — ішкі айқыш бұрыштары тең болса, онда а || b болатынын дәлелдейік.
АВ кесіндісінің ортасын О деп белгілейік. а және b түзулері параллель емес, керісінше олар Р нүктесінде қиылысады деп алайық (82.2-сурет).
Тең фигураларды бір-біріне беттестіруге болатыны белгілі. ∠1 = ∠2 және ОА = ОВ болғандықтан, оларды бір-біріне дәл келетін етіп беттестіруге болады. Осы мақсатта а, b, с түзулерін О нүктесінен 180°-қа бұрсақ, онда А және В нүктелері, АО және ОВ, АС және ВD, АЕ және ВD сәулелері, сонымен бірге а және b түзулері орындарын алмастырады (82.2-сурет).
Сонда АС және ВN сәулелерінің қиылысуында жатқан Р нүктесі ВD (АС) және АЕ (ВN) сәулелерінің қиылысуында жататын Q нүктесіне ауысады. Нәтижесінде, Р, Q нүктелері арқылы бір-біріне дәл келмейтін а, b екі түзуі өтеді. Бұл 12 негізгі қасиетке қайшы. Сондықтан а, b түзулері қиылыспайды, ендеше олар параллель. Теорема дәлелденді.
Теореманы ∠3, ∠4 — ішкі айқыш бұрыштарын қарастырып та дәлелдеуге болатыны түсінікті.
3 Теорема
3-теорема. Егер екі түзу ушінші түзумен қиылысқанда 1) ішкі тұстас бұрыштардың қосындысы 180°-қа тең болса; 2) сәйкес бұрыштар тең болса, онда берілген екі түзу параллель болады.
Бұл теореманы 2-теореманың көмегімен жеңіл дәлелдеуге болады.
Дәлелдеу. Алдымен теореманы ∠2 және ∠4 ішкі тұстас бұрыштар үшін дәлелдейік (82.1-сурет). Теореманың шарты бойынша ∠2 + ∠4 = 180°, бірақ ∠1 + ∠4 = 180°. Осы екі теңдіктен ∠1 = ∠2 шығады. Бұл жағдайда теорема орындалады (2-теореманы қара). Демек, ∠2 + ∠4 = 180° болғанда, а || b болады.
Енді теореманы ∠1 және ∠5 сәйкес бұрыштар үшін дәлелдейік. Теореманың шарты бойынша ∠1 = ∠5. Вертикаль бұрыштар болғандықтан, ∠2 = ∠5. Соңғы екі теңдіктен ∠I = ∠2 шығады. Бұл жағдайда теорема орындалады. Демек, ∠I = ∠5 болғанда, а || b.
Сұрақтар
1. Егер түзу берілген түзулердің әрқайсысына параллель болса, онда қандай түзулер берілген?
2. Теоремаларды дәлелдеуде қандай аксиомалар мен теоремалар туралы білімдеріңді пайдаландыңдар?
Жаттығулар
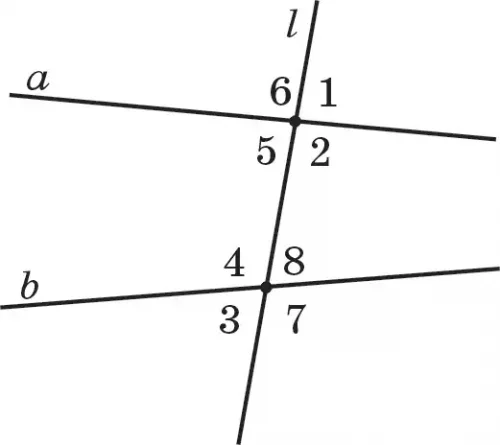
159. с түзуі кез келген а және b түзулерімен киылысқанда 8 бұрыш пайда болады (83-сурет). Олар цифрлармен белгіленген. Мұндағы 1) ∠2 = 95°, ∠4 = 100°. ∠5 пен ∠8 бұрьштарын табыңдар; 2) ∠2 + ∠8 = 160° екені белгілі. 5 және 4 бұрыштарының қосындысын табыңдар; 3) ∠4 — ∠5 = 15° екені белгілі, 2 және 8 бұрыштарының айырымын табыңдар.
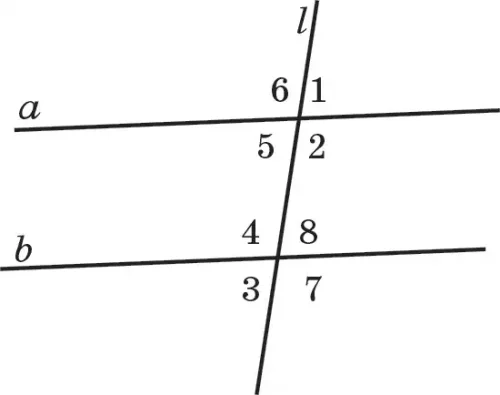
160. а мен b түзулері параллель, ал I түзуі оларды қиып өтеді (84-сурет). Пайда болған бұрыштар үшін 1) ∠I = ∠З; 2)∠1 = ∠8; 3)∠6 = ∠7; 4) ∠7 + ∠I = 180° екенін дәлелдеңдер.
161. Екі параллель түзуді үшінші түзумен қиғанда пайда болған бұрыштардың бірі 65°-қа тең. Қалған бұрыштарын табыңдар.
162. Екі параллель түзу үшінші түзумен қиылған. Ішкі тұстас бұрыштардың айырымы 40° екені белгілі. Түзулердің қиылысуында пайда болған барлық бұрыштарды табыңдар.
163. Екі параллель түзу үшінші түзумен қиылған. Ішкі айқыш бұрыштардың қосындысы 160°-қа тең. Түзулер қиылысқанда пайда болған барлық бұрыштарды табыңдар.
164. Екі параллель түзу үшінші түзумен қиылған. Сыртқы айқыш бұрьпптардың қосындысы 150°-қа тең. Түзулердің қиылысуында пайда болған бұрьпптарды табындар.
165. Екі параллель түзу үшінші түзумен қиылысқанда пайда болған бұрыштардың бірі 120°. Осы бұрыштың биссектрисасы екінші түзумен қандай бұрьпп жасап қиылысады?
166. АВ мен СD түзулері МN түзуімен қиылысканда, А және С нүктелері МN түзуінің бір жағындағы жарты жазықтықта, ал В және D нүктелері екінші жарты жазықтықта жатады. МN түзуі АВ түзуімен L нүктесінде, ал СD түзуімен К нүктесінде киылысады. ∠МКD = ∠МLВ. АВ және СD түзулері параллель болатынын дәлелдеңдер.
167. Екі параллель түзу және қиюшы түзу берілсе, онда 1) ішкі айкыш бұрыштардың биссектрисалары параллель; 2) сәйкес бұрыштардың биссектрисалары параллель; 3) ішкі тұстас бұрыштардың биссектрисалары перпендикуляр екенін дәлелдеңдер.