Понятие геометрической фигуры
Понятие геометрической фигуры. Геометрия изучает форму и размеры предметов. Предметы, различимые только по этим свойствам, принято называть геометрическими фигурами. Например, мяч имеет форму шара. Мяч реальный предмет, шар — геометрическая фигура. Многие геометрические фигуры вам уже известны. Например, точка, прямая, плоскость, окружность, треугольник, круг, шар, куб, прямоугольный параллелепипед, пирамида.
Любую фигуру мыслят в геометрии как множество точек. Геометрические фигуры бывают плоскими (рис.1.1) и неплоскими (рис.1.2). Плоской буде называть такую фигуру, все точки которой принадлежат одной плоскости.
Раздел геометрии, в котором изучают свойства только плоских фигур, называют планиметрией.


Смысл новых понятий в геометрии дается в определениях. Определением называется описание смысла нового понятия через ранее известные понятия. Например, для определения понятия квадрата используются ранее известные понятия: отрезок, равенство отрезков, прямой угол и др. Для определения каждого последующего понятия также используются ранее известные понятия. В геометрии имеются понятия, которые даются без определения. К ним относятся точка, прямая, плоскость. Понятия, принимаемые без определения, называются основными понятиями. А все остальные понятия определяются через эти основные понятия. Поскольку основным понятиям не даются определения, то они считаются известными. Чтобы показать точки на рисунке, их обозначают заглавными латинскими буквами А, В, С,… .
Например, точки А, В, С (рис. 2.1) .


Чтобы провести прямую, пользуемся линейкой.
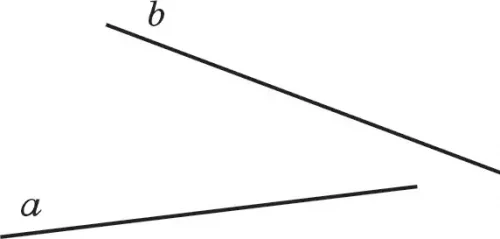
Прямую обозначают строчными латинскими буквами а, b, с, … . Например, прямые а, b, с (рис. 2.2).
Прямую можно продолжать бесконечно в обе стороны, а на рисунках показывается лишь ее часть.
Плоскость можно представить как поверхность стола, стены, классной доски и т. д. Однако они являются лишь частью плоскости. В действительности плоскость бесконечна во все стороны. Изображение плоскости показано на рис. 3.
Плоскость обозначают греческими буквами: α, β, γ… . Так как в курсе планиметрии (от греч. planum — “плоскость”) все фигуры рассматриваются на плоскости, далее не требуется изображать на каждом чертеже плоскость, она считается уже данной.
Рассмотрим взаимное расположение точек и прямой. Отметим на прямой а точку М (рис. 4).


В этом случае точка М лежит на прямой а. Другими словами, точка М принадлежит прямой а, лежит на прямой а, или прямая а проходит через точку М. Этот факт кратко обозначается следующим образом: М ∈ а. На рис. 4 точка В не лежит на прямой а, другими словами, точка В не принадлежит прямой а. Это кратко обозначается так: В ∉ а.
Обозначив на плоскости точку А, спомощью линейки проведем несколько прямых а, b, с,…, проходящих через эту точку (рис. 5).
Из рисунка видно, что через одну точку можно провести бесконечное
множество прямых. В этом случае можно сказать, что прямые а, b, с, … пересекаются в точке А. Пусть на плоскости даны точки А и В. Проведем прямую так, чтобы одно ребро линейки охватывало эти точки. Мы увидим, что через точки А и В можно провести только одну прямую (рис. 6).

Эта прямая обозначается через АВ. Значит, прямую можно обозначать и двумя заглавными буквами. Рассмотренные выше утверждения о взаимном расположении точек и прямой верны, и их правильность очевидна. Поэтому они излагаются в виде аксиом. Для того чтобы дать определение понятия аксиомы, необходимо познакомиться с понятием доказательства утверждения.
Аксиомы и доказательства
Поэтапное рассуждение о справедливости данного утверждения называется его доказательством. Утверждение, истинность которого не требует доказательства, называется аксиомой.
В данном случае следует охарактеризовать основные связи между неопределяемыми понятиями. Эти связи осуществляются с помощью применения таких слов, как “лежат”, “лежат между”. Иногда вместо слова “лежат” применяется слово “принадлежит”.
Остановимся на свойствах взаимосвязи точки и прямой на плоскости. В геометрии эти свойства составляют первую группу аксиом и называются аксиомами принадлежности.
А1. Какова бы ни была прямая, есть точки, принадлежащие и не принадлежащие ей.
А2. Через любые две точки можно провести прямую, причем только одну.
Опираясь на вышесказанные основные свойства, можно сделать следующие заключения:
1) по свойству А1 на любой прямой можно отметить произвольную точку. Таких точек бесконечно много. Из этого следует, что на прямой находится бесконечное множество точек;
2) различные две прямые, лежащие в одной плоскости, не имеют двух общих точек, т. е. если две прямые пересекаются, то они имеют только одну общую точку.
Если считать, что две прямые а и b на плоскости пересекаются в двух точках А и В, тогда через эти точки проходили бы две прямые а и b. Это противоречит свойству А2. Таким образом, две прямые одной
плоскости пересекаются в одной точке или не пересекаются;
3) с помощью линейки через две точки, лежащие в одной плоскости, можно провести прямую. По свойству А2 эта прямая единственная и она полностью принадлежит данной плоскости. Поэтому, если две точки прямой лежат в одной плоскости, то все ее точки лежат в этой плоскости.
Вопросы
1. В чем состоит необходимость введения основных понятий в геометрии? 2. Как вводятся новые понятия? 3. Какое отличие имеется между аксиомой и определением?
Упражнения
1. На рис. 7 изображены точки и прямые. Запишите точки и прямые, применяя нужные обозначения.
2. Проведите прямую а и отметьте на ней точки К, L, М. Данную прямую обозначьте через эти точки.
3. Отметив точки А и В, проведите прямую, проходящую через эти точки. Обозначьте эту прямую двумя буквами. Эту же прямую обозначьте одной буквой.
4. На рис. 7 изображены точки и прямые. Определите: 1) какие из точек лежат на прямых а и b; 2) какие точки не лежат на данных прямых.
5. Какие из точек, изображенных на рис. 8, лежат на прямой а, а какие на прямой b? Какие не лежат на этих прямых? Напишите с помощью нужных обозначений.
6. Изобразите на рисунке М ∈ а и В ∉ b.


7. Прямая а проходит через точку Х и не проходит через точку Y. Какая из этих точек лежит на прямой а ?
8. Обозначив точку М, проведите прямую с через эту точку. Сколько еще можно провести прямых, проходящих через эту точку?
9. Даны прямые а и b (рис. 9). Постройте точку их пересечения С. Взяв точки А,В соответственно на прямых а и b, обозначьте данные прямые двумя буквами.
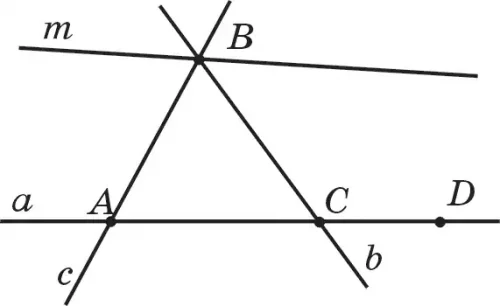
10. По рис. 10 ответьте на следующие вопросы: 1) Каким прямым принадлежат точка А , точка В, точка С, точка D? 2) Какие прямые проходят через точку А, точку В, точку С, точку D?
3) В какой точке пересекаются прямые а и b, b и с, с и т, b и т?
11. Дана прямая а. Используя аксиомы I1,I2, покажите, что можно провести и другие прямые.
12. Могут ли две различные прямые иметь: 1) одну общую точку; 2) две общие точки? Рассмотрите все возможные случаи.
13. Начертите две пересекающиеся прямые АВ и АС. 1) Обозначьте их точку пересечения; 2) совпадает ли прямая ВС с прямыми АВиАС? (Сделайте соответствующий чертеж.)
14. Нарисуйте четыре попарно пересекающиеся прямые. Обозначьте все точки пересечения этих прямых. Сколько получилось таких точек? Рассмотрите все возможные случаи.
15. Даны точки А, В, С, D, Е, не лежащие на одной прямой. Проведите различные прямые, каждая из которых проходит через две из указанных пяти точек. Сколько всего прямых можно провести?