Равные фигуры в геометрии
В курсе геометрии рассматриваются и равные фигуры.
Для того чтобы определить равенство двух фигур, нужно их наложить друг на друга. Для этого нужно выбрать соответствующие точки и элементы. Например, для того чтобы показать равенство четырехугольников АВСD и А′В′С′D′, нужно наложить четырехугольник АВСD на четырехугольник А′В′С′D′ так, чтобы их соответствующие точки совпали. Если при этом вершина А совпадет с вершиной А′; сторона АВ совпадет со стороной А′В′, а также совпадут другие соответствующие вершины и стороны, то тогда четырехугольники АВСD и А′В′С′D′ будут равны.
Определение. Фигуры называются равными, если при наложении их друг на друга соответствующие точки совпадут.
Равенство фигур F1 и F2 записывается так: F1 = F2.
Рассмотрим равенство отрезков.
Определение. Два отрезка называются равными, если при наложении друг на друга их концы совпадут.



Пусть даны отрезки АВ и А′В′ (рис. 23.1 ). Если при наложении точки А отрезка АВ на точку А′ отрезка А′В′ точки В и В′ совпадут, тогда отрезки АВ и А′В′ равны. Обозначают это так: АВ = А′В′. Понятие равных отрезков дает возможность построения отрезка, равного данному отрезку, отложив его на луче от начала луча. Если дан отрезок, то найдется отрезок, равный данному, один конец которого будет совпадать с началом луча, а другой конец — лежать на луче.
Если при наложении отрезка АВ на отрезок А′В′ так, чтобы точки А и А′ совпали, а точки В и В′ не совпадут, то возможны два случая. Первый, если точка В′ лежит между точками А и В, то АВ > А′В′ (рис. 23.2). Тогда АВ = АВ′ + В′В. Второй, если точка В лежит между точками А и В′, то АВ< А′В′ (рис. 23. 3). Тогда АВ =АВ′ – ВВ′.
Измерение отрезков
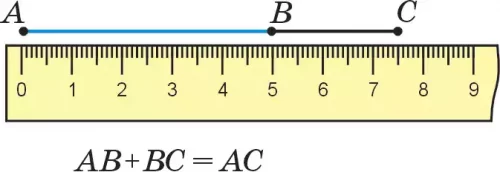
Для измерения длины отрезка можно использовать линейку с делениями. На рис. 24 длина отрезка АС равна 75 мм; это можно записать так: АС = 75 мм. Здесь за единицу измерения взят 1 мм. Значит, для измерения длины отрезка сначала нужно выбрать единицу измерения. Отрезок, равный единице измерения, называется единичным отрезком.
Итак, длину отрезка можно выразить любым положительным числом, а рядом с числом записывается единица измерения.
Тогда АС = 75 мм означает, что единичный отрезок, равный 1 мм, на отрезке АС отложен 75 раз. Значит, для того чтобы найти длину данного отрезка, надо найти число, определяющее, сколько единичных отрезков содержится в данном отрезке.
Длину отрезка АС по-другому можно назвать расстоянием между точками А и С. На рис. 24 видно, что длина отрезка АВ равна 50 мм, а отрезка ВС — 25 мм. Тогда длина отрезка АС равна сумме длин отрезков АВ и ВС, т. е.
АС = АВ +ВС = 50 мм +25 мм =75 мм.
Как следует из рис. 24, сумма длин отрезков АВ и ВС равна длине отрезка АВ.
Для измерения длины отрезка можно использовать и циркуль. Выберем произвольный единичный отрезок длиной 2 см. Для того чтобы измерить длину отрезка СD (рис. 25), отложим с помощью циркуля, начиная
от точки С, вдоль луча СD отрезки длиной 2 см. Если до точки D единичный отрезок отложен 6 раз, то
нетрудно вычислить, что длина СD будет равна: СD = 6 · 2 см =12 см.

Аксиомы измерения отрезков
Из этого следует, что длину отрезка можно умножить на определенное число. Опираясь на ранее сказанное о равенстве отрезков, приводим аксиомы измерения отрезков.
Они образуют III группу аксиом.
III1. Каждый отрезок имеет определенную длину, большую нуля.
III2.Если точка, принадлежащая отрезку, лежит между его концами, то длина данного отрезка равна сумме длин образовавшихся отрезков.
Таким образом, для того чтобы найти длину отрезка, полученного умножением длины данного отрезка на определенное число, нужно первоначальную длину данного отрезка умножить на данное число.
Вопросы
1. Приведите примеры на применение равенства фигур. 2. Как вы думаете, всегда ли отрезок содержит целое число единичного отрезка? Ответ обоснуйте. 3. Всегда ли можно измерить отрезок любой длины с помощью циркуля при заданном единичном отрезке? Рассмотрите все возможные случаи.
Упражнения
28. Начертите отрезок. С помощью циркуля отложите отрезок, равный этому отрезку.
29. Из разноцветной бумаги вырежьте равные квадраты АВСD и А1В1С1D1. Как можно проверить их равенство?
30. Вырежьте из бумаги квадрат АВСD и разделите его по диагонали АС. Убедитесь в равенстве полученных треугольников.
31. На рис. 26 изображены равные фигуры F и F1. Перемещая вдоль какой прямой, их можно наложить друг на друга?
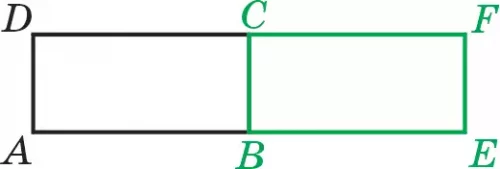
32. В прямоугольнике АВСD длина 3 см, ширина 1,5 см (рис. 27). После его перемещения вдоль стороны АВ на 3 см получен прямоугольник ВЕFС. Будут ли прямоугольники АВСD и ВЕFС равными? Если да, то почему?
33. Даны точки М, N, D, лежащие на одной прямой (рис. 28). 1) Какая точка лежит между двумя другими?
2) Какой отрезок определяет сумму отрезков МN и ND?

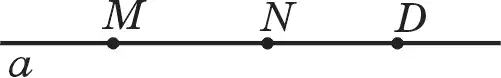
3) Какой отрезок определяет разность отрезков МD и ND?
34. Дан квадрат АВСD. Определите, какие из отрезков АВ, ВС, СD, DА, АС, ВD: 1) равны; 2) имеют общую точку; 3) не имеют общей точки. Покажите на рисунке.
35. Даны единичный отрезок СD и отрезок АВ. Если отрезок СD можно отложить на отрезке АВ, начиная от точки А, 3 раза, то чему равна длина отрезка АВ? Как это можно записать? Чему равна длина отрезка, если СD = 1 дм?
36. На отрезке МN длиной 12 см, начиная от точки М, отложим 4 раза отрезок длиной 2 см, при этом получим точку К. Найдите длины отрезков МК и КN.
37. Даны отрезки АВ = 20 м, АС = 5 м, ВD = 7,9 м. Найдите длину отрезка СD, если: 1) точки С и D лежат на отрезке АВ; 2) точки С и D не лежат на отрезке АВ; 3) только точка С лежит на отрезке АВ; 4) только точка D лежит на отрезке АВ.
38. Точки А,В,С лежат на одной прямой: АВ = х, АС = х – 2. Может ли точка В лежать между точками А и С?
39. Точки А, В,С лежат на одной прямой. Точка А лежит между точками В и С. АВ = х, АС = х + 4,3; ВС = 6,7. Найдите длину отрезка АС.
40. Даны точки С, D и М, лежащие на одной прямой. Точка М лежит между точками С и D. Если СМ = а + 1, DМ = а + 2 (а>0), то может ли длина отрезка СD быть больше 3?
41. Квадрат, состоящий из 16 клеток, разделите на две равные части тремя равными отрезками.
42. Как можно убедиться в равенстве сторон квадрата?