Кесінді
Геометрияда кесінді және сәуле ұғымдары көп қолданылады. Олар түзудің бөліктері ретінде анықталады. Түзуде шексіз көп нүктелердің жатқаны белгілі. Ол нүктелер түзуде қандай тәртіппен орналасады? Бұл сұраққа жауап беру үшін а түзуін және осы түзуде жататын А, В және С нүктелерін алайық (11-сурет).

Мұнда С нүктесі А және В нүктелерінің арасында жатады дейміз. Бірақ В нүктесі А және С нүктелерінің арасында жатады деп айтуға болмайды. Өйткені А және С нүктелері В нүктесінің бір жағында, сол сияқты В және С нүктелері А нүктесінің бір жағында жатады. Шындығында, арасында деген ұғым арқылы нүктелердің түзуде орналасуының қасиетін баяндауға болады. Ол баяндаулар геометрияда реттік аксиомалары деген атпен берілген бір топ аксиомалардан (II топ) тұрады.
II1.Түзудегі үш нүктенің біреуі және тек біреуі гана ңалган екеуінің арасында жатады.
“Арасында жатады” деген ұғым кесінді ұғымын анықтауға мүмкіндік береді.
Анықтама. Түзудің берілген екі нүктесі мен олардың арасында жатқан барлық нүктелерінен тұратын бөлігін кесінді деп атайды.
Берілген екі нүкте кесіндінің ұштары деп аталады. 11-суретте түзудің А, В нүктелері және олардың арасында жатқан барлық нүктелер түзудің бөлігін, яғни кесіндіні анықтап тұр. Бұл кесіндіні АВ немесе ВА арқылы белгілейді. А және В нүктелері—АВ кесіндісінің ұштары. Түзудің нүктелері шексіз көп болгандықтан, кесіндінің нүктелері де шексіз көп. А және В нүктелерінің арасында жататын С нүктесін әрқашан да табуға болады.
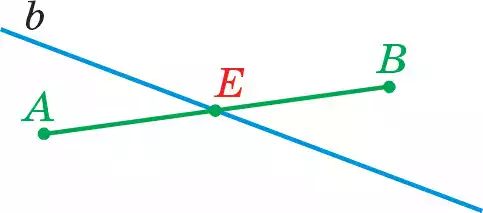
Егер АВ кесіндісі мен b түзуінің ортақ Е нүктесі бар болса, онда АВ кесіндісі мен b түзуі Е нүктесінде қиылысады, яғни Е нүктесі b түзуінде де, АВ кесіндісінде де жатады (12-сурет).
Сәуле
с түзуі берілсін (13-сурет). с түзуінен алынған О нүктесі оны екі бөлікке бөледі, олардың әрқайсысы жарты түзу деп аталады. А, В нүктелері жарты түзудің бірінде, ал С, В нүктелері екіншісінде жатыр. Мұндағы О жарты түзулердің бас нуктесі деп аталады.

Бүдан О нүктесі жарты түзулердің бірінде жатқан кез келген екі нүктенің (мысалы, А, В нүктелерінің немесе С, D нүктелерінің) арасында жатпайтынын байқаймыз, себебі ол жарты түзулердің басы болып табылады. Жоғарыда аталған ұғымдар негізінде нүктелердің түзуде орналасуының екінші аксиомасын береміз.
II2.Түзуде жатқан нүкте сол түзуді екі жарты түзуге бөледі.
Жарты түзуді сәуле деп те атайды.
13-суретте келтірілген жарты түзуді не сәулені екі әріппен белгілейміз. Мысалы, ОА және ОС. Мұнда алдыңғы әріп сәуленің бас нүктесін, ал екіншісі сәуленің бойындағы кез келген нүктені анықтайды. Сөйтіп, түзуде жатқан әрбір нүкте түзуді екі сәулеге бөледі. ОА, ОС сәулелері (13-сурет) бір-бірін түзуге дейін толықты-рып тұрады. Сондықтан оларды толықтауыш сәулелер деп атайды. Демек, сәулелер түзудің бөліктері болып табылады.
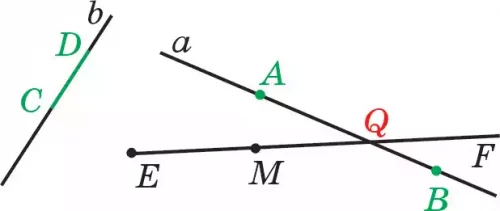
ЕҒ сәулесі берілсін (14-сурет). Бұл сәуленің бойынан М нүктесін белгілейік. Сонда М нүктесі ЕҒ сәулесінде жатыр, ал А нүктесі бұл сәуледе жатпайды.
Берілген ЕҒ сәулесінде ЕМ ке-сіндісі де жатыр. Сондықтан ЕМ ке-сіндісін ЕҒ сәулесінің бөлігі деп қа-растыруға болады. Егер кесіндінің (түзудің) берілген сәулемен ортақ нүктесі бар болса (болмаса), онда кесінді (түзу) мен сәуле қиылысады (қиылыспайды) деп айтылады.
Мысалы, 14-суретте берілген ЕҒ сөулесі АВ кесіндісімен (а түзуімен) Q нүктесінде қиылысқан, ал СD кесіндісімен (b түзуімен) қиылыспайды. Жазықтықта кез келген бір нүктені белгілеп алсақ, онда осы нүкте бас нүктесі болатын шексіз көп сөуле жүргізуге болады.
Егер берілген түзулердің екі ортақ нүктесі болса, онда олар беттеседі.
Жарты жазықтық
Енді жазықтықта жатқан түзу мен нүктелердің өзара орна-ласуын қарастырайық.
Қандай да бір жазықтық жөне сол жазықтықта жатқан а түзуі берілсін (15-сурет). а түзуі жазықтықты екі бөлікке бөледі. Бөліктердің әрқайсысы жарты жазыктык, деп аталады. Жарты жазықтықтардың бірін α1, екіншісін α2 арқылы белгілейік.
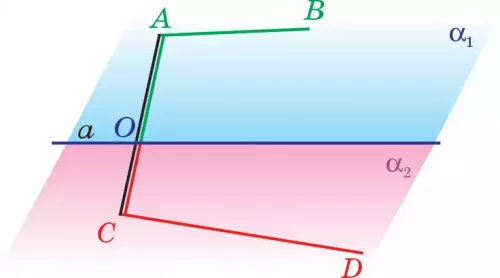
Мынадай ерекшеліктерге көңіл бөлейік. Егер А, В нүктелері бір жарты жазықтықта жатса, оларды қосатын АВ кесіндісі а түзуімен қиылыспайды. С, D нүктелері мен СD кесіндісі де дөл сол сияқты. Ал А жөне С нүктелері өртүрлі жарты жазықтықтарда (а1 жөне а2) жатыр. Оларды қосатын АС кесіндісі а түзуімен О нүктесінде қиылысады.
Осы айтылғандар негізінде жазықтықтағы нүктелердің түзуге қатысты орналасуының негізгі қасиетін көрсететін аксиома шығады. Ол екінші топтың аксиомаларына жатады.
II3. Түзу жазықтықты екі жарты жазықтыққа бөледі.
Бұл аксиоманың негізінде мынадай қорытынды жасауға болады. Жазықтықтагы қиылысқан екі тузудің толықтауыш сәулелері әртурлі жарты жазықтықтарда жатады. Жазықтықтағы а жөне b түзулері О нүктесінде қиылыссын (16-сурет). Сонда b түзуі екі сөулеге бөлінеді. Бұл сәулелер әртурлі жарты азықтықтарда жатады. ОА жөне ОС сөулелері — b түзуінің толықтауыш сәулелері. Егер ОА сәулесінен кез келген В нүктесін алсақ, О нүктесі А және В нүктелерінің арасында жатпайды, өйткені О нүктесі — ОА сәулесінің бас нүктесі. Сондықтан АВ кесіндісі а түзуімен қиылыспайды. Олай болса, ОА сәулесінде жатқан кез келген А, В, … нүктелері жарты жазықтықтардың біреуінде жатады. Онда ОА сәулесі α1 жарты жазықтығында жатыр.

ОА және ОС сәулелері толықтауыш сәулелер болғандықтан, О нүктесі А және С нүктелерінің арасында жатыр. Демек, С ∈ α2. Онда ОС сәулесінің барлық нүктелері α2 жарты жазықтығында жататынын жоғарыдағыдай көрсетуге болады. Нәтижесінде, ОС сәулесі α2 жарты жазықтығында жатыр.
Сөйтіп, b түзуінің ОА, ОС толықтауыш сәулелері а жазықтығындағы а түзуі арқылы бөлінген әртүрлі жарты жазықтықтарда жатыр.
Сұрақтар
1. Кесінді мен сәуленің қандай ұксастығы мен өзгешеліктері бар? 2. Кесінді мен түзу, сәуле мен түзу, кесінді мен сәуле өзара қалай орналасу-лары мүмкін? Барлық жағдайды сурет арқылы көрсетіңдер.
Жаттығулар

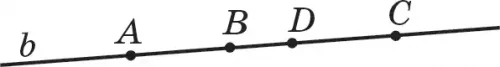
16. Бір түзуде жатпайтын М, N, Р нүктелерін белгілеңдер. Олардың әрбір екі нүктесі арқылы өтетін 1) кесінді салыңдар; 2) түзулер жүргізіңдер. Оларды әріптермен белгілеңдер; 3) әрбір екі түзудің қиылысу нүктесін көрсетіңдер. М нүктесі NР кесіндісінде жата ма?
17. М нүктесінде қиылысатын а және b түзулерін салыңдар. Пайда болған жарты түзулерді көрсетіңдер.
18. Түрлі түсті қарындаштарды пайдаланып, 17-суретті дәптерлеріңе көшіріп салыңдар. Қиылысатын және қиылыспайтын сәулелерді анықтаңдар. Қиылысатын болса, қиылысу нүктелерін, бөліктерін көрсетіңдер.
19. а түзуінде жататын А, В, С нүктелері берілген (17-сурет). Олар-дың қайсысы қалған екеуінің арасында жатады? С нүктесі А мен В нүктелерінің арасында жатады деп айтуға бола ма?
20. b түзуінде жататын А, В, С, D төрт нүкте берілген (18-сурет). Олардың ішінен 1) қалған екеуінің арасында жататын нүктелерді; 2) қалған екеуінің арасында жатпайтын нүктелерді атаңдар.


21. 19-сурет бойынша 1) а түзуінің бойында жатқан барлық кесінділерді жазыңдар; 2) В нүктесі қай кесіндіде жатыр? 3) D нүктесі АВ кесіндісінде жата ма?
22. А нүктесі а түзуін АВ және АС жарты түзулеріне бөледі (19-сурет). 1) Жарты түзулердің біреуінде жататын екі нүктені көрсетіңдер. 2) Әртүрлі жарты түзулерде жататын нүктелерді көрсетіңдер.
23. 19-суретте 1) барлығы неше сәуле бар? 2) D нүктесінің бір жағында қандай нүктелер орналасқан? Әртүрлі жағында ше? 3) D нүктесі қандай нүктелердің арасында жатыр?
24. 20-суреттен өзара қиылысатын жарты түзулерді көрсетіңдер.
25. Бір түзуде жатпайтын А, В, С нүктелері берілген (21-сурет). Олардың әрбір екеуі арқылы түзу жүргізіңдер. 1) Қанша түзу жүргізілді? Оларды әріптермен белгілеңдер. 2) Түзулердің қиылысу нүктелерін анықтаңдар. 3) Бас нүктесі А, В, С нүктелерінде болатын сәулелерді атаңдар.
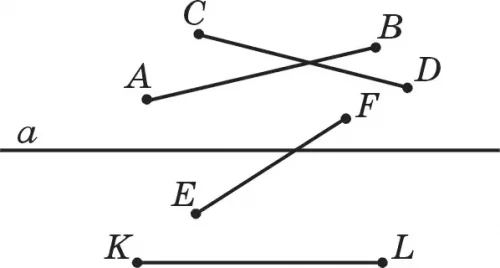
26. Жазықтықта жатқан а түзуі және АВ, СD, ЕҒ, КL кесінділері берілген (22-сурет). а түзуі берілген жазықтықты α1 және α2 жарты жазықтықтарға бөледі.
1) Түрлі түсті қарындашты пайдаланып, кесінділердің орналасуын кескіндеңдер. 2) Бір жарты жазықтықта жатқан кесінділерді көрсетіңдер. 3) Қай кесінділер а түзуімен қиылысады және қай кесінділер қиылыспайды? 4) Өзара қиылысатын кесінділерді және қиылыспайтын кесін-ділерді анықтаңдар.
27. Бір түзудің бойында 1) неше кесінді; 2) неше сәуле болады?