Перпендикулярные прямые
Рассмотрим две пересекающиеся прямые.
Пусть при пересечении в точке О прямые АВ и СD образуют прямой угол (рис. 46). Заметим, ∠ВОD = 90°, ∠DОА = 90°, ∠СОВ= 90°, ∠АОС= 90°. В этом случае прямые АВ и СD будут перпендикулярными. ( От лат. перпендикулярис — “вертикальная линия”.)
Определение. Две прямые, пересекающиеся под прямым углом, называются перпендикулярными.
Перпендикулярность прямых обозначается символом “⊥”.
Утверждение “Прямая а перпендикулярна прямой b” записывается так:
а ⊥ b. И отрезки, и лучи, лежащие на перпендикулярных прямых, также
будут перпендикулярны. То есть лучи ОВ и ОD, а также отрезки ОЕ,
ОN, изображенные на рис. 46, считаются перпендикулярными.
Отметим, что две прямые, перпендикулярные к третьей, не пересекаются.

В самом деле, рассмотрим прямые СС1 и DD1, перпендикулярные к прямой АВ (рис. 47,1). Мысленно перегнем рисунок по прямой АВ так, чтобы верхняя часть рисунка наложилась на нижнюю. Так как
прямые углы 1 и 2 равны, то луч АС наложится на луч АС1. Аналогично, луч ВD наложится на луч ВD1. Поэтому, если предположить, что прямые СС1 и DD1 пересекаются в точке Е, то эта точка наложится на некоторую точку Е1, также лажащую на этих прямых (Рис.47,2), и мы получим, что через точки Е и Е1 проходят две прямые: СС1 и DD1. Но это не возможно. Следовательно, наше предположение неверно и, значит, прямые СС1 и DD1 не пересекаются.


Теорема 1
Теорема 1. Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Доказательство. Пусть В — точка, не лежащая на прямой СD (рис.48.1). Докажем сначала, что из точки В можно провести перпендикуляр к прямой СD. Отложим от луча СD угол NСD, равный углу ВСD, как показано
на рисунке 48,1. Так как углы ВСD и NСD равны, то первый из них можно наложить на второй так, что стороны СВ и СD первого угла совместятся со сторонами СN и СD второго угла.
Наглядно это наложение можно представить себе как перегибание рисунка по прямой СD. При этом точка В наложится на некоторую точку В1 луча СN. (рис. 48.2). Обозначим буквой А точку пересечения прямых СD и ВВ1. Отрезок ВА и есть искомый перпендикуляр прямой СD. В самом деле, при указанному наложений (перегибании рисунка) луч АВ совмещается с лучом АВ1, поэтому угол 1 совмещается с углом 2. Следовательно, ∠1=∠2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Поэтому, ВА ⊥ СD.



Докажем теперь, что из точки В можно провести только один перпендикуляр к прямой СD. Если предположить, что через точку В можно провести еще один перпендикуляр ВА
1 к прямой СD, то получим, что две прямые ВА и ВА1, перпендикулярные к прямой СD, пересекаются (рис.49). Но выше было доказано, что это невозможно.
Итак, из точки В можно провести только один перпендикуляр к прямой СD.
Теорема доказана.
Теорема 2
Теорема 2. Через любую точку прямой можно провести лишь одну прямую, перпендикулярную данной.
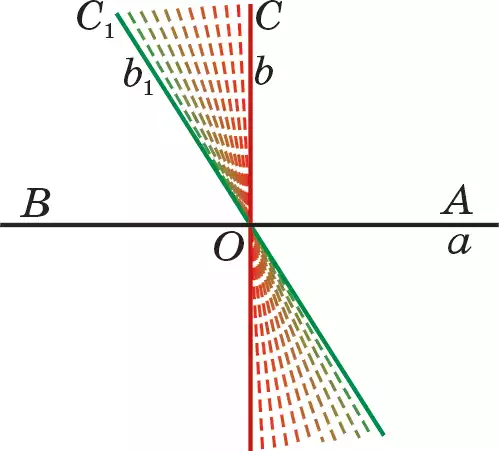
Доказательство. Дана прямая а (рис. 50). Возьмем на этой прямой любую точку О. В одной из полуплоскостей относительно прямой а от луча ОА отложим ∠АОС= 90°. Тогда ОС⊥ ОА. Если построим дополнительный луч ОD к лучу ОС, то получим прямую b. Значит, b ⊥ а. Теперь покажем, что существует только одна прямая b, проходящая через точку О и перпендикулярная прямой а. Предположим, что в полуплоскости, содержащей луч ОС, существует еще один луч ОС1, который определяет прямую b1 ⊥ ОА, перпендикулярную прямой а. Тогда ∠АОС 1 = 90°. Но по аксиоме IV2 в данной полуплоскости от данного луча ОА можно отложить лишь один угол, равный 90°. Из этого следует, что лучи ОС1 и ОС или прямые b1 и b совпадут. Итак, существует лишь одна прямая b, проходящая через любую точку О прямой а и перпендикулярная к ней. Теорема доказана.

Теорема 3
Теорема 3. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную данной, причем только одну.
Доказательство. Даны прямая а и точка В, не лежащая на ней (рис. 51).
Через точку В проведем прямую b, параллельную прямой а. Через точку В проведем прямую с так, что b ⊥ с. Тогда получается, что с и а пересекаются в точке А. Выходит, что существует единственная прямая, проходящая через точку В и перпендикулярная прямой а. Допустим обратное, что существует еще одна прямая с1. Тогда две прямые с, с1, перпендикулярные прямой b, пересекутся в точке В, а это противоречит теореме 3. Значит, через точку В можно провести только одну прямую, перпендикулярную а. Теорема доказана.
Отрезок ВА, опущенный из точки В на прямую а, будем называть перпендикуляром, а отрезок ВС — наклонной (рис. 51). Точка А называется основанием перпендикуляра ВА, а точка С — основанием
наклонной ВС. Отрезок АС является проекцией наклонной ВС на прямой а. Длина отрезка ВА называется расстоянием от точки В до прямой а.
Вопросы
1.Знание каких аксиом и теорем использовалось при доказательстве теорем?
Упражнения
88. Дана прямая а. С помощью транспортира проведите прямую b, перпендикулярную прямой а.
89. Даны прямая а и точка А, не лежащая на этой прямой. Проведите прямую b, перпендикулярную прямой а, проходящую через точку А. Используйте чертежный треугольник.
90.Три угла, образовавшихся при пересечении двух прямых а и b, равны между собой. Докажите, что а ⊥ b.
91. Докажите, что перпендикуляр и наклонная, проведенные к одной прямой, пересекаются.
92. Перпендикулярные прямые АВ и СD пересекаются в точке О. Лучи ОЕ и ОF лежат в одной полуплоскости с лучом ОD. Если ∠ЕОF =105° и ∠ВОF = 28°, то вычислите ∠DОF и ∠ЕОD.
93. Даны два угла с общей вершиной, причем один острый, другой — тупой. Соответствующие стороны этих углов перпендикулярны. Докажите равенство двух образовавшихся острых углов.
94. Даны два угла с общей вершиной, соответствующие стороны которых перпендикулярны. Один из них меньше второго в 4 раза. Найдите эти углы.
95. Прямые КМ и LN пересекаются в точке О, причем КМ ⊥ LN. Проведен луч ОD, который с лучом ОК образует угол, равный 58°. Между лучами ОМ и ОL проведен луч ОР так, что ∠РОМ + ∠LОD = 75°. Лучи ОD, ОL, ОР лежат в одной полуплоскости относительно прямой КМ. Найдите ∠РОМ и ∠LОD.