Геометриялық фигура түсінігі
Геометриялық фигура түсінігі. Геометрия заттардың пішінін және өлшемдерін зерттейді. Осындай қасиеттері бойынша ғана айыруға болатын заттарды геометриялың фигуралар деп атайды. Мысалы, доптың пішіні шар тәрізді. Доп — нақты зат, ал шар — геометриялық фигура. Көптеген геометриялық фигуралармен сендер бұрыннан таныссыңдар. Мысалы, нүкте, түзу, жазықтық, шеңбер, үшбұрыш, дөңгелек, шар, куб, тікбұрышты параллелепипед, пирамида.
Геометрияда кез келген фигураны нүктелер жиыны деп қарастырады. Геометриялық фигуралар жазық (1.1-сурет) және жазық емес (1.2-сурет) болып бөлінеді. Барлық нүктелері бір жазықтықта жататын фигура жазық фигура деп аталады. Геометрияның тек қана жазық фигуралардың қасиеттерін зерт-тейтін бөлімін планиметрия деп атайды. Геометрияда жаңа ұғымдарға анықтамалар беріледі. Жаңа ұғымдардың мағынасын бұрыннан белгілі ұғымдар арқылы түсіндіретін сөйлемді аныңтама деп атаймыз. Мысалы, төртбұрышты анықтау үшін бұрыннан белгілі нүкте, кесінді ұғымдары пайдаланылады.
Жалпы, кез келген жаңа ұғымды анықтау үшін оған дейін белгілі ұғымдар қолданылады.


Геометрияда кейбір ұғымдарға анықтама бере алмаймыз, өйткені одан бұрын анықталған ұғым жоқ. Сондықтан оларды анықтамасыз қабылдауға тура келеді. Ондай ұғымдарға нукте, түзу, жазықтық жатады.
Анықтамасыз қабылданатын ұгымдар негізгі ұгымдар деп аталады.
Ал қалған ұғымдардың барлығы да сол негізгі ұғымдар арқылы тікелей немесе жанама түрде анықталады. Негізгі ұғымдарға анықтама берілмейтіндіктен, олар белгілі деп есептеледі.
Нүктелерді сызбада көрсету үшін оларды латынның А, В, С… бас әріптерімен белгілейді. Мысалы, А, В, С нүктелері (2.1-сурет).


Сызбада түзуді сызып көрсету үшін сызғышты қолданамыз.
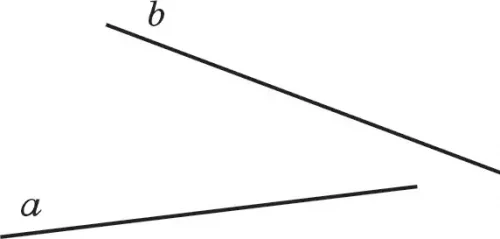
Түзуді латынның а, Ь, с, … кіші әріптерімен белгілейді (2.2-су-рет). Түзу шексіз. Сондықтан біз суретте түзудің бөлігін ғана сызып көрсете аламыз.
Үстелдің бетін, терезе әйнегінің бетін, тақтаның бетін жазықтық-тар деп қарастыруға болады. Бірақ олар да жазықтықтардың бөліктері ғана. Ал кез келген жазықтықты барлық төрт жағына шексіз созуға болады. 3-суретте жазықтықтар кескінделген. Жазықтықтарды гректің а (альфа), в (бета), ү (гамма) және т.б. әріптерімен белгілейді. Планиметрия (латынның planum сөзінен алынған, жазықтық деген ұғымды білдіреді) курсында барлық фигуралар бір ғана жазықтықта қарастырылады, сондықтан сызбада жазықтықты арнайы кескіндеп көрсету талап етілмейді, ол берілген деп есептеледі.
Алдымен нүкте мен түзудің өзара орналасуына тоқталайық. Нүктені жазықтықта қалауымызша белгілеп алуға болады, сол себепті оны түзу бойында да, түзуден тыс та көрсете аламыз. а түзуінің бойынан М нүктесін белгілейміз (4-сурет).


Бұл жағдайда М нүктесі а түзуінде жатады. Басқаша оны, М нүктесі а түзуіне тиісті немесе а түзуі М нүктесі арқылы өтеді деп те айтамыз және қысқаша М е а түрінде белгілейміз. Ал 4-суретте берілген В нүктесі а түзуінде жатпайды, басқаша айт-қанда, В нүктесі а түзуіне тиісті емес, оны қысқаша В∉ а түрінде белгілейді.
Жазықтықта А нүктесін белгілеп, сызғыштың көмегімен осы нүкте арқылы өтетін бірнеше а, b, с,… түзулерін жүргізейік (5-сурет).
Демек, бір нүкте арқылы өтетін шексіз көп түзу сызуға болады. Бұл жағдайда а, b, с, … түзулері А нүктесінде қиылысады деп айтылады.
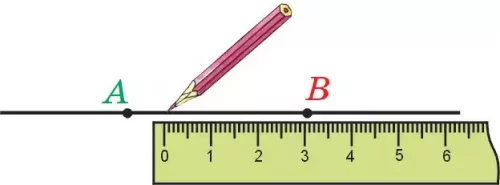
Жазықтықта А және В нүктелері берілсін, сызғыштың бір жиегін осы нүктелермен дәл келетін етіп ұстап, түзу сызамыз (6-сурет).
Сонда А, В нүктелері арқылы өтетін бір ғана түзу сызуға болатынын көреміз. Оны қысқаша АВ түзуі деп белгілейміз. Яғни, түзуді екі әріппен де белгілейді.
Жоғарыда қарастырғандай, нүктелер мен түзулердің өзара орналасуына байланысты айтылған сөйлемдер өзінен-өзі түсінікті болғандықтан, дәлелдеусіз қабылданады. Сондықтан олар аксиома-лар түрінде баяндалады.
Аксиома ұғымына анықтама беру үшін, алдымен тұжырымдаманы дәлелдеу ұғымымен танысайық.
Берілген тұжырымдаманы ретімен талдау арқылы ақиқат-тыгына көз жеткізу оны дәлелдеу деп аталады.
Ақиқаттыгы дәлелдеусіз қабылданатын сөйлем аксиома деп аталады.
Мұндағы анықтамасыз алынған анықталмайтын ұғымдардың арасындағы негізгі байланыстарды сипаттауға тура келеді. Ондай байланыстар жатады, арасында жатады деген сөздерді қолдану арқылы жүзеге асырылады. Кейде жатады деген сөздің орнына тиісті сөзі қолданылады.

Аксиомалар және дәлелдер
Енді жазықтықтағы нүктелер мен түзулердің бір-біріне тиісті болатыны туралы қасиеттерге тоқталайық.
Олар геометрияда негізгі қасиеттердің бірінші тобын құрайды да, тиістілік аксиомалары деп аталады. Ол аксиомалар мыналар:
I1. Қандай түзуді алсақ та, ол түзуге тиісті нүктелер де, оған тиісті емес нүктелер де бар болады.
I2. Кез келген екі нүкте арқылы бір ғана түзу жүргізуге болады.
Аталған негізгі қасиеттерге сүйеніп, төмендегі қорытындылар-ды жасаймыз:
1) 11 қасиетке сүйеніп, кез келген түзудің бойынан қалауымызша нүкте алуға болады. Олар шексіз көп.
2) Жазықтықтағы әртүрлі екі түзуде ортақ екі нүкте болмайды. Басқаша айтқанда, екі түзуге ортақ тек бір ғана нүкте табылуы мүмкін, яғни екі түзу бір нүктеде қиылысуы мүмкін.
Егер жазықтықта берілген а мен b түзулері А және В нүктелерін-де қиылысады деп есептесек, онда А және В нүктелерінің әрқайсысы арқылы екі а және b түзулері өткен болар еді. Бұл 12 қасиетке қайшы келеді. Демек, жазықтықтағы екі түзу бір ғана нүктеде қиылысады немесе олар қиылыспайды.
3) Жазықтықта берілген екі нүкте арқылы өтетін түзу сызуға болады. 12 қасиет бойынша ондай түзу біреу ғана және ол түзу толығымен берілген жазықтықта жатады. Сондықтан түзудің екі нүктесі жазықтықта жатса, онда оның барлық нүктелері де сол жазықтықта жатады. Басқаша айтқанда, түзу толығымен жазық-тықта жатады.
Сұрақтар
- Планиметрияның негізгі ұғымдарын берудің қажеті неде? 2. Жаңа ұғымдар қалай енгізіледі? 3. Анықтама мен аксиоманың айырмашылығы неде?
Жаттығулар
1. 7-суретте нүктелер мен түзулер кескінделген. Олардың белгі-ленуін жазып көрсетіңдер.
2. а түзуін сызып, оның бойына К, L, М нүктелерін белгілеңдер. Осы нүктелер арқылы түзуді белгілеп жазыңдар.
3. А және В нүктелерін белгілеп, олар арқылы өтетін түзуді жүр-гізіңдер. Түзуді осы екі нүкте арқылы белгілеп жазыңдар. Осы түзуді бір әріппен де белгілеп көрсетіңдер.
4.7-суретте көрсетілген нүктелердің қайсысы а түзуінде, қайсысы b түзуінде жатады? Қайсы нүктелер қандай түзудің бойында жатпайды? Жауаптарын тиісті белгілеулерді пайдаланып жазыңдар.


5.8-суретте көрсетілген нүктелердің қайсысы а түзуінде, қайсысы b түзуінде жатады? Қандай нүктелер бұл түзулерде жатпайды? Жауаптарын ∈ не ∉ белгілерін пайдаланып жазыңдар.
6.М ∈ а және В ∉ b деген жазулар суретте қалай көрсетілуі мүмкін?
7.а түзуі X нүктесі арқылы өтеді, ал Ү нүктесі арқылы өтпейді. Осы нүктелердің қайсысы а түзуінде жатады?
8.М нүктесін белгілеп, ол арқылы өтетін с түзуін жүргізіңдер. Осы нүкте арқылы өтетін тағы да қанша түзу жүргізуге болады?
9.а және b түзулері берілген (9-сурет). Олардың қиылысу нүктесі болатын С нүктесін салыңдар. а, Ь түзулерінен сәйкес А, В нүктелерін алып, берілген түзулерді екі әріп арқылы белгілеп жазыңдар.
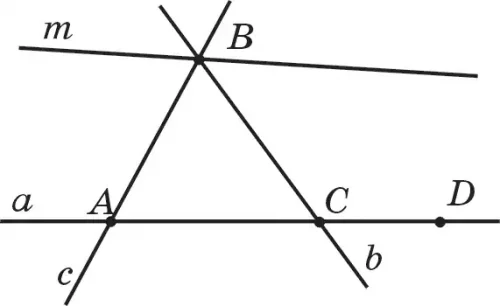
10.10-сурет бойынша мына сұрақтарға жауап беріңдер:
1) А, В, С, D нүктелерінің әрқайсысы қай түзулерде жатады?
2) А, В, С, D нүктелерінің әрқайсысы арқылы қандай түзулер өтеді?
3) а мен b, b мен с, с мен m және b мен m түзулері қай нүктелерде қиылысады?
4) Бір нүкте арқылы қандай үш түзу өтеді?
11.а түзуі берілген. 11, 12 аксиомаларын пайдаланып, басқа да түзулер жүргізуге болатынын көрсетіңдер.
12.Әртүрлі екі түзудің ортақ 1) бір нүктесі; 2) екі нүктесі болуы мүмкін бе? Барлық мүмкін жағдайларды қарастырыңдар.
13.АВ және АС — қиылысатын түзулер. 1) Олардың қиылысу нүктесін белгілеңдер; 2) ВС түзуі АВ түзуімен де, АС түзуімен де дәл келмейтінін түсіндіріп беріңдер (сәйкес сызбаны өздерің жасаңдар).
14.Өзара екі-екіден қиылысатын төрт түзу жүргізіңдер. Осы түзулердің қиылысу нүктелерін белгілеңдер. Неше қиылысу нүктесі болуы мүмкін? Мүмкін болатын нұсқаларын қарастырыңдар.
15.Бір түзуде жатпайтын А, В, С, D, Е нүктелері берілген. Осы нүктелердің әрбір екеуі арқылы өтетін түзулерді жүргізіңдер. Барлығы неше түзу жүргізуге болады?