Теорема 1-2
Алдыңғы өтілген тақырыптардан тікбұрышты үшбұрышпен таныссыңдар. Енді осы үшбұрыштың қасиеттері қарастырылады. Қаңдай жағдайда тікбұрышты үшбұрыштар тең болады екен?
1-теорема. Егер екі тікбұрышты үшбұрыштың 1) сәйкес катеттері тең болса 2) сәйкес бір катеті және оған іргелес жатқан сүйір бұрышы тең болса 3) гипотенузалары және оған іргелес жатқан бір сүйір бұрыштары тең болса, онда бұл үшбұрыштар тең болады.
Дәлелдеу. Үшбұрыштар теңдігінің I белгісінің негізінде 1) мен 2) жағдай, ал II белгісінің негізінде 3) жағдайдың ақиқаттығы дәлелденеді. Үшбұрыштың ішкі бұрыштарының қосындысы туралы теореманың 5-салдарынан тікбұрышты үшбұрыштардың сүйір бұрыштарының бірі өзара тең болса, онда екінші сүйір бұрыштары да тең болатынын білесіңдер.
2-теорема. Егер бір тікбұрышты үшбұрыштың катеті мен гипотенузасы екінші тікбұрышты үшбұрыштың сәйкес катеті мен гипотенузасына тең болса, онда мұндай тікбұрышты. үшбұрыштар тең болады.
Тікбұрышты АВС және А’В’С‘ үшбұрыштарында АВ = А’В‘, ВС = В’С‘ болсын (69-сурет). ΔАВС = ΔА’В’С‘ екенін дәлелдеу керек.
Дәлелдеу. СА сәулесіне толықтауыш сәуле жүргізіп, оның бойына С‘А‘ қабырғасына тең болатын кесінді саламыз. В мен С1 нүктелері қосылса, А‘‘ё үшбұрышына тең С1ВС үшбұрышы пайда болады (1-теорема, 1-жағдай). Мұндағы, С1 В = А ‘В ‘ = АВ, ∠1 = ∠2. Ал С1В = АВ болғандықтан, ΔАВС1 — теңбүйірлі үшбұрыш. Сондықтан ∠3 = ∠2 = ∠1. Олай болса, ΔАВС = ΔА’‘ё (1-теорема). Теорема дәлелденді.
Теорема 3-4


3-теорема. Кез келген үшбұрыштың үлкен қабырғасына қарсы үлкен бұрыш жатады.
ΔАВС берілсін және а > b болсын. ∠А > ∠В екенін дәлелдеу керек (70-сурет).
Дәлелдеу. СВ = а, СВ сәулесівде СD = b болатын D нүктесін аламыз. а > b болғандықтан, D нүктесі СВ кесіндісінде жатады. Онда АD сәулесі А бұрышының ішінде жатады, яғни
∠2 < ∠А (1)
Салуымыз бойынша ΔАDС теңбүйірлі болғандықтан,
∠2 = ∠1 (2)
∠1 — АВD үшбұрышының сыртқы бұрышы.
∠В < ∠1 (3)
(үшбұрыштың сыртқы бұрыштарының қосындысы туралы теоре-ма, 2-салдар). (1), (3), (2) теңдіктен ∠В < ∠А шығады. Теорема дәлелденді.
4-теорема (3-теоремаға кері теорема). Кез келген үшбұрыштың үлкен бұрышына қарсы үлкен қабырғасы жатады.
4-теореманың дәлелдеуін өздерің ұсыныңдар. 3-, 4-теоремалардан мынадай салдарлар шығады.
1-салдар. Тікбұрышты үшбұрыштың кез келген катеті оның гипотенузасынан кіші болады.
2-салдар. Нүктеден түзуге түсірілген перпендикуляр сол нүкте-ден жүргізілген көлбеуден кіші болады.
1- және 2-салдарды өздерің дәлелдеңдер.
Теорема 5
5-теорема. Үшбұрыштың кез келген қабырғасы оның басқа екі ңабырғасының қосындысынан кем болады.
АВС үшбұрышы берілсін (71-сурет). АВ < АС + ВС екенін дәлелдеу керек.
Дәлелдеу. Кесінділердің ұзындықтарын өлшеу арқылы бұл теңсіздіктің орындалатыны көрсетілген болатын. Сәуле бойына С нүктесі- А нен бастап СD = ВС болатын СD кесіндісін саламыз (III1). Нәтижесінде
АD = АС + СD = АС + ВС (1)
шығады. ВDС теңбүйірлі үшбұрыш болғандықтан,
∠1 = ∠2 (2)
С нүктесі А мен D нүктелерінің арасында жатыр. Сондықтан ВС сәулесі АВD бұрышының ішінде жатады:
∠АВD > ∠1 (3)
2) мен (3)-тен ∠АВD > ∠2 шығады. Ендеше, АВD үшбұрышында АВ < АD (4-теорема). Олай болса, (1) теңдік былай жазылады:
АВ < АС + ВС (4)
Теорема дәлелденді.



Мысалдар
1-мысал. Тікбұрышты үшбұрышта 30°-қа қарсы жатқан катет гипотенузаның жартысына тең (72-сурет).
Шешуі. Теңқабырғалы АВС үшбұрышының АВС бұрышы 60°-қа тең болсын. ВD биссектрисасын жүргізелік. Ол үшбұрышқа әрі медиана, әрі биіктік болғандықтан ВDС үшбұрышы тікбұрышты үшбұрыш, яғни

2-мысал. 73-суретте ΔАВС = ΔҒЕD және АВ = ҒЕ, ∠1 = 135°.
ВСҒ бұрышының шамасын табыңдар.
Шешуі. Шарт бойынша
ΔАВС = ΔҒЕD және АВ = ҒЕ, бұдан ΔВСА = ∠ЕDҒ. ∠ЕDҒ = 180° — 135° = 45° = ∠ВСА. ∠ВСА + ∠ВСҒ = 180°, ∠ВСҒ = 180° — 45° = 135°.
∠2 = 135° (4)
теңсіздік үшбұрыштың кез келген қабырғасы үшін орындалады.
Сұрақтар
1. Екі тікбұрышты үшбұрыштар тең болуы үшін олардың катеттерінің теңдігі жеткілікті болу себебі қандай?
2. Тікбұрышты үшбұрыштар теңдігін дәлелдеу үшін олардың сәйкес екі элементінің теңдігін көрсету жеткілікті болуы неліктен?
3. Кез келген үш кесіндіден үшбұрыш кұрастыруға бола ма? Жауаптарыңды негіздеңдер.
Жаттығулар
140. Катеттерін бір түсті, гипотенузасын басқа түсті қарындашпен тікбұрышты үшбұрыш сызыңдар. Әр түсті қарындашпен гипотенузаға жүргізілген биссектриса, медиана, биіктігін көрсетіңдер.
141. АВС теңбүйірлі үшбұрышын сызыңдар. D және Е нүктелерін АС қабырғасынан АD = СЕ болатын етіп алыңдар. DВЕ үшбұрышы қандай үшбұрыш болады?
142. АВС — тікбүрышты теңбүйірлі үшбұрыш (∠С = 90°). АВ, ВС және СА қабырғаларының орталары сәйкесінше D, Е, Ғ нүктелері-мен белгіленіп, DС, DЕ, DҒ кесінділері жүргізілген. 1) Суретте неше үшбұрыш пайда болды? 2) D нүктесінің берілген үшбұрыштың төбелерінен бірдей қашықтықта болатынын дәлелдеңдер.
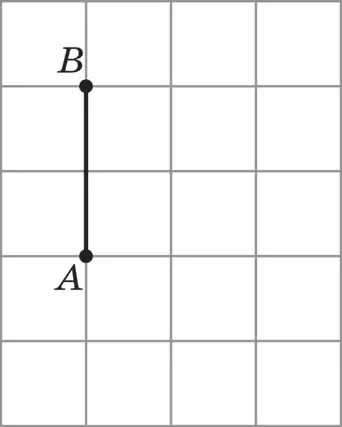
143. Гипотенузасы АВ кесіндісі болатын, ал С төбесі тордың бір түйінінде жататын тікбұрышты үшбұрыш салыңдар (74-сурет).
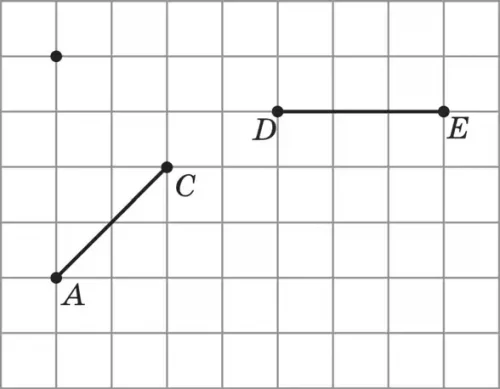
144. АС кесіндісі катет болатындай, ал С төбесі тордың бір түйінінде жататындай тікбұрышты үшбұрыш салыңдар. Тордың әр таяқшасы 1-ге тең деп алып, гипотенузасын табыңдар (75-сурет).
145. DЕ кесіндісі катет болатындай, ал Ғ төбесі тордың бір түйінінде жататындай тікбұрышты үшбұрыш салыңдар. Тордың әр таяқшасы 1-ге тең деп алып, катеттің ұзындығын табыңдар (75-сурет).
146. Теңбүйірлі үшбұрыштың бүйір қабырғаларына түсірілген биіктіктері тең болатынын дәлелдеңдер.
147. Егер үшбұрыштың бүйір қабырғаларына түсірілген биіктіктері тең болса, онда оның теңбүйірлі үшбұрыш болатынын дәлелдеңдер.
148. Түзуге одан тыс жатқан нүктеден екі көлбеу жүргізілген. Көлбеулердің табандарының арақашықтығы 12,4 дм. Көлбеулердің түзудегі проекцияларын табыңдар.