Теоремалар

Үшбұрыштар теңдігінің I, II белгілеріне сүйеніп, бірнеше теоремалар дәлелдеуге болады.
1-теорема. Теңбүйірлі үшбұрыштың табанындағы бұрыштары тең болады.
Берілген АВС үшбұрышындағы (63-сурет) АС, ВС — бүйір қабырғалары, АВ — табаны, ∠3 пен ∠4 — табанына іргелес жатқан бұрыштар болсын. ∠3 = ∠4 болатынын дәлелдейік.
Дәлелдеу. СD — биссектрисасы жүргізілсін, онда үшбүрыштар теңдігінің I белгісі бойынша ∠АСD = ∠ВСD болады (АС = ВС, СD ортақ, ∠А = ∠2).
Бұдан ∠3 = ∠4 екені шығады. Теорема дәлелденді.
2-теорема. Теңбүйірлі үшбұрыштың табанына жүргізілген биссектриса оның әрі медианасы, әрі биіктігі болады.
Дәлелдеу. 1-теорема бойынша ∠АСD = ∠ВСD теңдігінен АD = ВD шығады, ендеше СD — медиана. Сол сияқты ∠АDС = ∠ВDС, олай болса ∠АDС = ∠ВDС = 90° (∠АDС мен ∠ВDС — жазыңқы бұрыштың жартысы). Ендеше, СD — үшбұрыштың биіктігі. Теорема дәлелденді.
Біз теңбүйірлі үшбұрышта табанына жүргізілген биссектрисасы, медианасы және биіктігі беттесетінін көрсеттік. Сондықтан келесі тұжырымдар орындалады: 1. Теңбүйірлі үшбұрыштың табанына жүргізілген биіктігі оған әрі медиана, әрі биссектриса болады.
2. Теңбүйірлі үшбұрыштың табанына жүгізілген медианасы оган әрі биіктік, әрі биссектриса болады.
Үшбұрыштардың 3-ші теңдік белгісі
3-теорема (үшбұрыштар теңдігінің III белгісі). Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда мұндай үшбұрыштар тең болады.
АВС және А’В’С‘ үшбұрыштары берілсін. АВ = А‘В’, ВС = ‘ђ, СА = С‘А‘ (64-сурет). ΔАВС = ΔА ‘В‘ С‘ болатынын дәлелдеу керек.
Дәлелдеу. Жазықтықтың А‘В‘ түзуімен бөлінген және С’ жатпайтын жартысында А‘В‘ сәулесінен бастап ∠ВАС = ∠В‘А‘С1 болатын А‘Е сәулесі жүргізілсін (64-сурет). Сонан кейін А‘ Е сәулесінің бойына А‘С1 = АС = А‘С‘ болатын етіп А‘С1 кесіндісі салынсын. Сонда үшбұрыштар теңдігінен
ΔАВС = ΔА‘ В‘ С1 (1)
аламыз.
Бұдан ВС = В‘С1 = ‘ё және ∠АСВ = ∠А‘С1 В‘ шығады. С‘ пен С1 нүктелері А‘В‘ түзуіне қатысты әртүрлі жарты жазықтықтарда жатады. Сондықтан С‘С1 кесіндісі А‘В‘ түзуін қиып өтеді (II3 аксиома). Қиылысу нүктесі D болсын. АВС үшбұрышының түріне байланысты D нүктесі А‘В‘ кесіндісінде немесе сол кесінді жатқан сәуленің бойында жатуы немесе В‘ нүктесімен беттесуі мүмкін.
D нүктесі А‘В‘ кесіндісіне тиісті болсын (64-сурет), А‘С‘С1 мен ‘ёС1 теңбүйірлі үшбұрыштар болғандықтан, ∠1 = ∠2, ∠З = ∠4 (1-теорема).
Олай болса, ∠1 + ∠З = ∠2 + ∠4 немесе ∠А‘ё‘ = ∠А‘С1В‘.
Ендеше, үшбұрыштар теңдігінің I белгісі бойынша
ΔА‘ В‘ С‘ = ΔА‘ В‘ С1 (2)
аламыз.
(1) мен (2) теңдіктерден: ΔАВС = ΔА‘ В‘ С‘.
D нүктесі А‘В‘ сәулесіне тиісті болсын (65-сурет).
Жоғарыда айтылтан белгілеулер мен түсініктерді пайдалансақ, ∠А‘С‘D = ∠1, ∠А‘С1 D = ∠2, ∠‘ёD = ∠З, ∠В‘С1 D = ∠4 болады. Мұндағы ∠1 = ∠2, ∠З = ∠4. В‘ нүктесі А‘ пен D нүктелерінің арасында жатыр, сондықтан ё‘ сәулесі ∠1-дің ішінде, ал С1 В’ сәулесі ∠2-нің ішінде жатады.
Олай болса, ∠А‘ё‘ = ∠1 — ∠З, ∠А‘С1 В‘ = ∠2 — ∠4. Осыдан ΔА‘‘ё = ΔА‘ С1 В‘.
Үшбұрыштар теңдігінің I белгісі бойынша
ΔА‘ В‘ С‘ = ΔА‘ В‘ С1. (3)



(1) мен (3) теңдіктерден ΔАВС = ΔА‘‘ё шығады.
D нүктесі В‘ нүктесімен дәл келген жағдайда (сызбасын өз беттеріңмен салыңдар), теореманың дәлелденуі жеңілденеді. Бүл жағдайда
ΔА‘ В‘ С‘ = ΔА‘ В‘ С1 (4)
болады. (1) мен (4) теңдіктерден ΔА‘ В‘ С‘ = ΔАВС шығады. Сонымен теорема толық дәлелденді.
Теңбүйірлі үшбұрыштың қасиеттерін қолдануға мысал келтірейік.
Мысал. 66-суретте АВ = ВС. ВАК бұрышы ВСD бұрышына тең болатынын көрсетіңдер.
Шешуі. АВ = ВС болғандықтан АВС үшбұрышына тең бүйірлі. Сондықтан табанының бұрыштары ретінде ВАС бұрышы мен ВСА бұрышы тең. Осыдан, тең бұрыштарға іргелес бүрыштар ретінде ∠ВАК = ∠ВСD.
Сұрақтар
1. Теңбүйірлі үшбұрыштың төбесінен табанына жүргізілген биссектриса неліктен әрі биіктік, әрі медиана болады?
2. Теңбүйірлі үшбұрыш үшін үшбұрыштар теңдігінің үшінші белгісін қалай тұжырымдауға болады?
Жаттығулар
127. Қабырғалары 1) 4 см, 6 см, 7 см; 2) 6 см, 9 см, 0,6 см; 3) 5 м, 5 м, 5 м; 4) 1,2 м, 7 м, 12 дм болатын үшбұрыштар берілген. Олардың қайсысы 1) теңбүйірлі;
2) теңқабырғалы; 3) әртүрлі қабырғалы үшбұрыш болады?
128. 178-есепте берілген үшбұрыштардың әрқайсысының периметрін табыңдар. Қандай үшбұрыштың периметрін есептеу жеңіл?
129. Теңбүйірлі үшбұрыштың 1) бүйір қабырғасы 8 см, табаны 10 см; 2) бүйір қабырғасы 5 м, табаны 7 м болғандағы периметрін табыңдар.
130. Теңбүйірлі үшбұрыштың периметрі 20,6 дм. 1) Табаны 6 дм болғандағы бүйір қабырғаларын; 2) бүйір қабырғасы 53 см болғандағы табанын; 3) табаны бүйір қабырғасынан 2,6 дм артық болғандағы қабырғаларын табыңдар.
131. Теңқабырғалы үшбұрыштың қабырғасы 6,2 см. Үшбұрыштың периметрін табыңдар.
132. Теңқабырғалы үшбұрыштың периметрі 32,4 дм. Оның қабырғасын табыңдар.
133. Теңқабырғалы үшбұрыштың бір қабырғасына жүргізілген медиана оны 8 дм және 8 дм бөліктерге бөледі. Үшбұрыштың қабырғаларын табыңдар.
134. Теңбүйірлі АВС үшбұрышының периметрі 60 дм, ВD — табанына түсірілген биіктік. АВD үшбұрышының периметрі 46 дм. ВD биіктігін табыңдар.
135. Жоғарыда 134-есепте берілген үшбұрыштың В төбесінен жүргізілген медианасы мен биссектрисасын табыңдар.
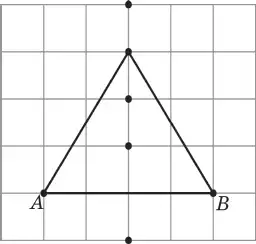
136. Табаны АВ кесіндісі, ал С төбесі тордың түйіндерінің бірінде болатын теңбүйірлі үшбұрыш салыңдар (67-сурет). Осындай қанша үшбұрыш бар?
137. Табаны АС кесіндісі, ал В төбесі тордың түйіндерінің бірінде болатын тең бүйірлі үшбұрыш салыңдар (68-сурет). Осындай қанша үшбұрыш бар?
138. Екі теңбүйірлі үшбұрыштың сәйкес табандары және оларға түсірілген биіктіктері тең болса, онда осы үшбұрыштардың тең болатынын дәлелдеңдер.
139. Теңқабырғалы үшбұрыштың барлық 1) медианалары; 2) биссек-трисалары; 3) биіктіктері тең болатынын дәлелдеңдер.