Теоремы
На основании 1-го и 2-го признаков равенства треугольников можно доказать ряд теорем.
Теорема 1. Углы при основании равнобедренного треугольника равны.
Доказательство. Пусть в данном ΔАВС АС = ВС (рис. 63). AВ — основание треугольника, ∠3 и ∠4 — углы при основании. Докажем, что ∠3 = ∠4. Проведем биссектрису СD, тогда по первому признаку равенства треугольников ΔАСD= ΔВСD (СD — общая сторона, АС= ВС, ∠2 = ∠1). Отсюда получается, что ∠3 = ∠4. Теорема доказана.

Теорема 2. Биссектриса, проведенная к основанию равнобедренного треугольника, является его и медианой, и высотой.
Доказательство. Воспользуемся теоремой 1. Так как ΔАСD= ΔВСD, то АD = ВD, следовательно, СD является медианой. Далее имеем, что ΔАDС = ΔВDС или ∠АDС = ∠ВDС = 90° (∠ВDС — половина развернутого угла). Тогда СD есть высота треугольника. Теорема доказана.
Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также утверждения:
1. Высота равно бедренного треугольника, проведенная к основанию,
является медианой и биссектрисой.
2. Медиана равно бедренного треугольника, проведенная к основанию,
является высотой и биссектрисой.
Рассмотрим решение задачи на применение свойства равнобедренного треугольника.
Пример. На рисунке ниже АВ=ВС. Докажите, что угол ВАK равен углу ВСD.
Р е ш е н и е . Треугольник АВС — равнобедренный, так как АВ=ВС. Следовательно, угол ВАС равен углу ВСА, как углы при основании равнобедренного треугольника. Отсюда следует, что угол ВАК равен углу ВСD как смежные углы соответственно равным углам.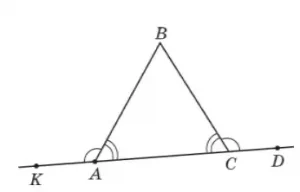
3-й признак равенства треугольников
Теорема 3 (3-й признак равенства треугольников).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Пусть даны треугольники АВС и А′В′С′, у которых АВ=А′В′, ВС=В′С′,СА=С′А′ (рис. 64).
Докажем, что ΔАВС = ΔА′В′С′. На полуплоскости относительно прямой А′В′, где не лежит точка С′, начиная от луча А′В′, построим луч А ′Е так, чтобы получилось ∠ВАС = ∠В′А′С 1 (рис. 64). Затем на луче А′Е можно отложить отрезок А′ С1 так, чтобы получилось А′С1 = АC = А′С′. Тогда на основании равенства треугольников
ΔАВС = ΔА′В′ С1. (1)
Откуда вытекает, что ВС = В′С1=В С′ и ∠АСВ= ∠А′С1В′. Точки С′ и С1 относительно прямой А′В′, лежат на разных полуплоскостях. Поэтому отрезок С′С1 пересекается с прямой А′В′ (аксиома II3).
Обозначим их пересечение точкой D.
В зависимости от вида треугольника АВС точка D может лежать на отрезке А′В′, или на его продолжении, или может совпадать с точкой В′. Пусть точка D лежит на отрезке А′В′ (рис. 64). Так как А′С′ С1 и В′С′С1 являются равнобедренными треугольниками, ∠1 = ∠2, ∠3= ∠4 (теорема 1). Отсюда получается, что ∠1 + ∠3 = ∠2 + ∠4 или ∠А′С′В′ = ∠А′С1В′.
Следовательно, на основании первого признака равенства треугольников ΔА′В′С′ = ΔА′В′С1. (2)
Из равенства (1) и (2) вытекает, что ΔАВС= ΔА′В′С′.
Пусть точка D лежит на продолжении отрезка А′В′ (рис. 65).



Если используем вышеуказанные обозначения и понятия, тогда ∠А′С′D = ∠1, ∠А′С
1D = ∠2, ∠ В′С′D = 3, ∠В′С1D = ∠4. Понятно, что ∠1 = ∠2, ∠3 = ∠4. Поскольку точка В′ лежит между точками А′ и D, то луч С′В′ лежит внутри ∠1, луч С1В′ лежит внутри ∠2. Поэтому ∠А′С′В′ = ∠1– ∠3, ∠А ′С 1В′ = ∠2 – ∠4. На основании этих двух равенств можно считать, что ΔА′В ′С′ = ΔА′С1В′.
Теперь, если применим первый признак равенства треугольников, тогда: ΔА′В′С′= ΔА′В′С1. (3)
Из равенства (1) и (3) получается, что ΔАВС= ΔА′В′С′.
Если точка D совпадает с точкой В′ (чертеж сделайте сами), тогда значительно облегчается доказательство теоремы. В этом случае сразу вытекает, что: ΔА′В′С′= ΔА′В′С1. (4)
Из равенств (1) и (4) получается, что ΔАВС = ΔА′В′С′. Следовательно, во всех трех случаях ΔАВС= ΔА′В′С′. Теорема доказана полностью.
Вопросы
1. Почему в равнобедренном треугольнике биссектриса, проведенная из вершины лежащего против основания угла, одновременно может служить и медианой и высотой? 2. Как можно сформулировать третий признак равенства треугольников для равнобедренных треугольников?
Упражнения
127. Стороны треугольника равны:
1) 4 см, 6 см, 7см; 2) 6 см, 9 см, 0,6 дм; 3) 5 м, 5 м, 5 м; 4) 1,2 м, 7 м, 12 дм.
В каком случае получается треугольник: 1) равнобедренный; 2) равносторонний; 3) разносторонний?
128. Найдите периметр каждого треугольника, данного в упражнении 178. Покажите, в каком случае возможно вычислить легким способом.
129. В равнобедренном треугольнике: 1) боковая сторона — 8 см, основание — 10 см; 2) боковая сторона — 5 м, основание — 7 м. Найдите периметр треугольника.
130. Периметр равнобедренного треугольника равен 20,6 дм. Если: 1) основание — 6 дм, то найдите его боковую сторону; 2) боковая сторона — 53 см, то найдите его основание; 3) основание больше, чем боковая сторона на 2,6 дм, то найдите его стороны.
131. Сторона равностороннего треугольника равна 6,2 см. Найдите его периметр.
132. Периметр равностороннего треугольника равен 32,4 дм. Найдите его сторону.
133. Медиана, проведенная на одну из сторон равностороннего треугольника, делит ее на две равные части длиной 8 дм. Найдите стороны треугольника.
134. Периметр равнобедренного ΔАВС равен 60 дм, ВD— его высота, опущенная на основание. Периметр ΔАВD — 46 дм. Найдите высоту ВD.
135. В заданном выше упражнении 134 найдите в треугольнике медиану и биссектрису, проведенную из вершины В.
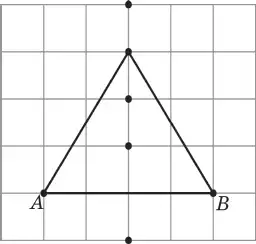
136. Нарисуйте какой-нибудь равнобедренный треугольник, основанием которого является отрезок AB, а вершина C расположена в одном из узлов сетки (Рис. 67). Сколько таких тругольников?
137. Нарисуйте какой-нибудь равнобедренный треугольник, основанием которого является отрезок AC, а вершина B расположена в одном из узлов сетки (Рис. 68). Сколько таких треугольников?
138. Если у двух равнобедренных треугольников и основания, и опущенные к ним высоты равны, то такие треугольники равны. Докажите.
139. Докажите, что в равностороннем треугольнике равны все его: 1) медианы; 2) биссектрисы; 3) высоты.