Кез келген үшбұрыштың iшкi бұрыштарының қосындысын мына теореманың негiзiнде табуға болады.
Теорема
Теорема. Үшбұрыштың ішкі бұрыштарының қосындысы 180°-қа тең болады.
Дәлелдеу. ΔАВС берілген. ∠1, ∠2, ∠3 оның ішкі бұрыштары болсын. С төбесі арқылы АВ қабырғасына параллель l түзуін жүргізейік. Аксиома бойынша l түзуі жалғыз ғана болады№
Үшбұрыштың АС қабырғасы өзара параллель АВ мен l түзулерінің, ал СВ өзара параллель l мен АВ түзулерінің басқа көлбеумен қиюшысы болып табылады, сонда пайда болған ішкі айқыш бұрыштар тең: ∠4 = ∠1, ∠5 = ∠2.
∠4 + ∠3 + ∠5 = 180° (жазынқы бұрыш) екені белгілі. Онда ∠1 + ∠2 + ∠3 = 180°. Теорема дәлелденді.
Анықтама. Үшбұрыштың ішкі бұрышымен сыбайлас бұрыш оның сыртқы бұрышы деп аталады.
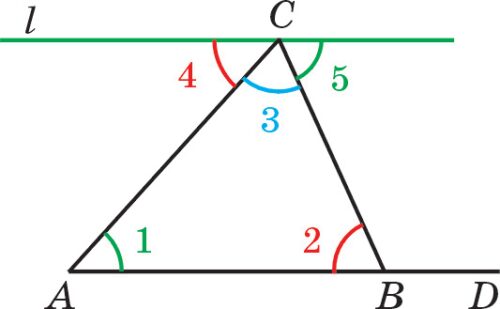
87 сүрет
87 — суреттегі АВС үшбұрыштың ∠2 ішкі бұрышымен сыбайлас бұрыш СВD, сондықтан ∠СВD сыртқы бұрыш болады.
Үшбұрыштың ішкі бұрыштарының қосындысы туралы теоремадан шығатын салдарларға тоқталайық.
1 — салдар. Үшбұрыштың сыртқы бұрышы өзімен сыбайлас емес екі ішкі бұрыштардың қосындысына тең болады.
1 — теорема бойынша ∠1 + ∠2 + ∠3 = 180°, бұдан
∠1 + ∠2 = 180° — ∠2. (1)
∠СВD — сыртқы бұрыш, олай болса ∠СВD + ∠2 = 180°, бұдан
∠СВD = 180° — ∠2. (2)
(1) мен (2) теңдіктерден
∠СВD = ∠1 + ∠3 (3)
шығады.
1 — салдар дәлелденді.
2 — салдар. Үшбұрыштың бір бұрышы ғана доғал (тік) бола алады.
3 — салдар. Тікбүрышты үшбұрыштың сүйір бұрыштарының қосындысы 90° — қа тең.
АВС үшбұрышында ∠С = 90° болсын. Теорема бойынша ∠А + ∠В + ∠С = 180° немесе ∠А + 90° + ∠В = 180°, бұдан ∠А + ∠В = 90°.
4 — салдар. Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың сәйкес екі бұрышына тең болса, онда олардың үшінші сәйкес бұрыштары да тең болады.
АВС мен А‘‘ё үшбұрыштары берілсін және ∠А = ∠А‘, ∠В = ∠В‘ болсын. Теорема бойынша ∠А + ∠В + ∠С = 180°, бұдан
∠С = 180° — ∠А — ∠В
немесе
∠С = 180° — ∠А‘ — ∠В‘. (1)
∠А‘ + ∠В‘ + ∠С‘ = 180°, осыдан
∠С‘ = 180° — ∠А — ∠В. (2)
(1) мен (2) теңдіктерден ∠С =∠С‘.
Олай болса, егер екі тікбұрышты үшбұрыштың бір сүйір бұрыштары тең болса, онда олардың екінші сүйір бұрыштары да тең.
1 — мысал. Сүйір бұрышы 45° -қа тең тікбұрышты үшбұрышта тік бұрыштың тқбесінен гипотенузаға түсірілген биіктіктің гипотенузасының жартысына тең болатынын дәлелдеңдер (88 — сурет).
Шешуі. АВС үшбұрышта ∠С = 90°, ∠А = 45° болсын. Үшбұрыштың ішкі бұрыштарының қосындысы туралы теорема бойынша
∠В + 45° + 90° = 180°, ∠В = 45°, яғни ΔАВС -теңбүйірлі: АС = ВС. СD биіктігін жүргізсек, теңбүйірлі АDС және
2 — салдар. Үшбұрыштың бір бұрышы ғана доғал (тік) бола алады.
3 — салдар. Тікбүрышты үшбұрыштың сүйір бұрыштарының қосындысы 90° — қа тең.
АВС үшбұрышында ∠С = 90° болсын. Теорема бойынша ∠А + ∠В + ∠С = 180° немесе ∠А + 90° + ∠В = 180°, бұдан ∠А + ∠В = 90°.
4 — салдар. Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың сәйкес екі бұрышына тең болса, онда олардың үшінші сәйкес бұрыштары да тең болады.
АВС мен А‘‘ё үшбұрыштары берілсін және ∠А = ∠А‘, ∠В = ∠В‘ болсын. Теорема бойынша ∠А + ∠В + ∠С = 180°, бұдан
∠С = 180° — ∠А — ∠В
немесе
∠С = 180° — ∠А‘ — ∠В‘. (1)
∠А‘ + ∠В‘ + ∠С‘ = 180°, осыдан
∠С‘ = 180° — ∠А — ∠В. (2)
(1) мен (2) теңдіктерден ∠С =∠С‘.
Олай болса, егер екі тікбұрышты үшбұрыштың бір сүйір бұрыштары тең болса, онда олардың екінші сүйір бұрыштары да тең.
1 — мысал. Сүйір бұрышы 45° -қа тең тікбұрышты үшбұрышта тік бұрыштың тқбесінен гипотенузаға түсірілген биіктіктің гипотенузасының жартысына тең болатынын дәлелдеңдер (88 — сурет).
Шешуі. АВС үшбұрышта ∠С = 90°, ∠А = 45° болсын. Үшбұрыштың ішкі бұрыштарының қосындысы туралы теорема бойынша
∠В + 45° + 90° = 180°, ∠В = 45°, яғни ΔАВС -теңбүйірлі: АС = ВС. СD биіктігін жүргізсек, теңбүйірлі АDС және
2 — салдар. Үшбұрыштың бір бұрышы ғана доғал (тік) бола алады.
3 — салдар. Тікбүрышты үшбұрыштың сүйір бұрыштарының қосындысы 90° — қа тең.
АВС үшбұрышында ∠С = 90° болсын. Теорема бойынша ∠А + ∠В + ∠С = 180° немесе ∠А + 90° + ∠В = 180°, бұдан ∠А + ∠В = 90°.
4 — салдар. Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың сәйкес екі бұрышына тең болса, онда олардың үшінші сәйкес бұрыштары да тең болады.
АВС мен А‘‘ё үшбұрыштары берілсін және ∠А = ∠А‘, ∠В = ∠В‘ болсын. Теорема бойынша ∠А + ∠В + ∠С = 180°, бұдан
∠С = 180° — ∠А — ∠В
немесе
∠С = 180° — ∠А‘ — ∠В‘. (1)
∠А‘ + ∠В‘ + ∠С‘ = 180°, осыдан
∠С‘ = 180° — ∠А — ∠В. (2)
(1) мен (2) теңдіктерден ∠С =∠С‘.
Олай болса, егер екі тікбұрышты үшбұрыштың бір сүйір бұрыштары тең болса, онда олардың екінші сүйір бұрыштары да тең.
1 — мысал. Сүйір бұрышы 45° -қа тең тікбұрышты үшбұрышта тік бұрыштың тқбесінен гипотенузаға түсірілген биіктіктің гипотенузасының жартысына тең болатынын дәлелдеңдер (88 — сурет).
Шешуі. АВС үшбұрышта ∠С = 90°, ∠А = 45° болсын. Үшбұрыштың ішкі бұрыштарының қосындысы туралы теорема бойынша
∠В + 45° + 90° = 180°, ∠В = 45°, яғни ΔАВС -теңбүйірлі: АС = ВС. СD биіктігін жүргізсек, теңбүйірлі АDС және ВDС екі үшбұрыш аламыз. Бұдан DС = АD = ВD.
2 — мысал. Табаны АВ болатын АВС үшбұрышы АD кесіндісімен екі теңбүйірлі үшбұрышқа бөлінген. Олар — табандары сәйкесінше АС мен ВD болатын АСD және АВD үшбұрыштары. АВС үшбұрышының бұрыштарын табыңдар.
Шешуі. Есептің шартынан ΔАВС — теңбүйірлі, АВ — табаны. АD кесіндісі АВС үшбұрышын екі теңбүйірлі үшбұрышқа бөледі (89 — сурет). Табу керегі А, В және С бұрыштары. Теңбүйірлі үшбұрыштың қасиеті бойынша АС = ВС; ∠А = ∠В. Үшбұрыштың ішкі бұрыштары туралы теорема бойынша ∠А + ∠В + ∠С = 180°.