Определение угла
С помощью понятий луча и деления плоскости прямой на части можно дать понятие угла.
Определение. Часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называется углом.
Лучи называются сторонами угла, а их начало называется вершиной. Угол обозначают с помощью знака “∠” и тремя заглавными буквами.
Буква, обозначающая вершину, записывается между двумя другими буквами.
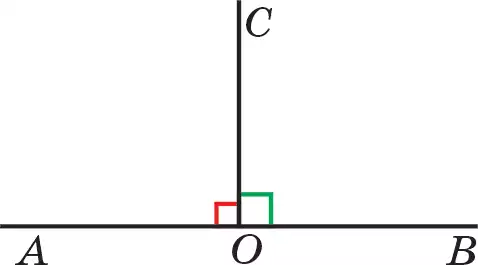
Например, на рис. 29.1 ∠АОВ или ∠ВОА (углы АОВ или ВОА).
Также угол можно обозначить одной буквой, являющейся его вершиной или же цифрой (рис. 29.2,3).
Как видите, угол на рисунке показывается дугой.
Равенство углов
Теперь рассмотрим равенство углов. Если градусные меры двух углов равны, то эти углы будут равны. Вообще равенство углов определяется следующим образом.
Определение. Два угла называются равными, если при наложении друг на друга их вершины и соответствующие стороны совпадут.
Например: ∠АВС и ∠DЕF, изображенные на рис. 30.1, равны (∠АВС = ∠DЕF), так как при наложении вершины В на вершину Е сторона ВА совпадает со стороной ЕD, также совпадают и стороны ВС и ЕF.
Дополним луч ЕD лучом ЕL до прямой (рис. 30.2). Тогда луч ЕF будет лежать на одной из полуплоскостей относительно прямой DL. Следовательно, угол, равный углу АВС, можно отложить от луча ЕDв одной полуплоскости (α1) относительно прямой LD.
Значит, если дан угол, то всегда можно найти равный ему угол, вершина и одна из сторон которого лежат на прямой, делящей плоскость на две части, а другая его сторона лежит на заданной полуплоскости.
Если при наложении угла АВС на угол DЕF на рис. 30 вершина В совпадает с вершиной Е, сторона ВА совпадает со стороной ЕD, а стороны ВС иЕF не совпадают, то возможны два случая. Первый, когда сторона ЕF ∠DЕF проходит между сторонами ВАи ВС угла АВС, тогда ∠АВС > ∠DЕF (рис. 31.1). Нетрудно увидеть, что в этом случае ∠АВС = ∠АВF + ∠FВС. Во втором случае сторона ВС ∠АВС проходит между сторонами ВА и ЕF ∠DЕF, тогда ∠АВС < ∠DЕF (рис. 31.2). В этом случае ∠АВС = ∠АВF – ∠FВС. ∠РОF и ∠FОN с общей стороной ОF равны, потому что луч ОF делит ∠РОN пополам (рис. 32).
Определения. Виды углов
Определение. Луч, исходящий из вершины угла и делящий его пополам, называется биссектрисой угла.
Теперь рассмотрим виды углов.
Определение. Угол, стороны которого являются дополнительными лучами, называется развернутым углом.
На рис. 33 показан развернутый угол DОС.
Пусть дан развернутый угол АОВ (рис. 34). Проведем луч ОС таким образом, чтобы он разделил этот угол на две равные части, т. е. ∠ВОС = ∠СОА.
Определение. Половина развернутого угла называется прямым углом.
На рис. 34 каждый из углов ВОС и АОС — прямой.
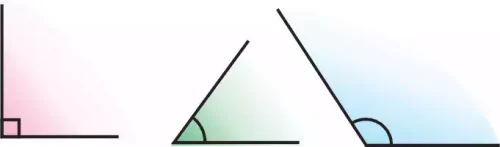
Определение. Угол, который меньше прямого угла, называется острым.
Определение. Угол, который больше прямого угла и меньше развернутого угла, называется тупым.
Итак, мы рассмотрели четыре вида углов: развернутый, прямой, тупой, острый (рис. 33, 35).
Измерение углов
Теперь рассмотрим измерение углов. С измерением углов вы знакомы из курса математики для 5 класса.
Чтобы измерить угол, сначала надо выбрать единицу измерения. Выше мы сравнивали углы с прямым углом. Поэтому угол удобно измерять, сравнивая с прямым углом. Разделив прямой угол на 90 равных частей, одну из частей, или 1/90 часть прямого угла, принимаем за 1 градус. Обозначая его 1° (1 градус), принимаем за единицу измерения угла.
Существуют и другие единицы измерения угла, которые называются минутой (′), секундой (′′), где 1°= 60′, 1′ = 60′′. Прямой угол равен 90 градусам, пишем 90°. Так как развернутый угол в 2 раза больше прямого угла, он равен 180°.
Для того чтобы узнать градусную меру острого и тупого углов, их следует измерить. Для измерения градусной меры углов используется транспортир.
На рис. 36 показаны измерения углов, равных 30°, 90°, 120°, с помощью транспортира. Результаты измерения запишем так: ∠ВОС = 30°, ∠ВОD = 90°, ∠ВОА = 120°. Если ∠ВОА состоит из суммы углов ВОD и DОА (рис. 36), то ∠ВОА=∠ВОD+ ∠DОА. Тогда сумма градусных мер углов ВОD и DОА равна градусной мере ∠ВОА, т. е. ∠ВОА = ∠ВОD + ∠DОА = 90° + 30° =120°. Здесь луч ОD проходит между сторонами ∠ВОА.
Следует отметить, что острый угол больше 0°, но меньше 90°, а тупой угол больше 90° и меньше 180°.
С помощью транспортира можно изобразить углы, градусные меры которых известны. Например, на рис. 37 показан способ построения угла КОD, равного 60°.
Аксиомы. Углы
Итак, из равенства углов и их измерения следуют основные свойства измерения углов. Они входят в третью группу аксиом.
III3. Каждый угол имеет определенную градусную меру, большую нуля.
III4. Если луч исходит из вершины угла и проходит между его сторонами, тогда данный угол равен сумме образовавшихся углов.
Выше было показано, как можно на луче, начиная с его начальной точки, отложить отрезок данной длины.
Также вы узнали, что можно построить угол, равный данному. Опираясь на эти понятия, можно сформулировать основные свойства отложения углов. Эти свойства образуют четвертую группу аксиом:
IV1. Каков бы ни был луч, начиная от его начальной точки, на нем можно отложить отрезок данной длины, и только одним способом.
IV2. От любого луча в заданную полуплоскость можно отложить угол заданной величины, меньшей 180°, и только один.
Вопросы
1. Может ли сумма двух острых углов быть больше или равной 180°? Ответ обоснуйте. 2. В чем сходство и различия свойств отложения отрезка и угла?
Упражнения
43. На разноцветной бумаге начертите острый, прямой и тупой углы, вырежьте и сравните их между собой. С помощью транспортира определите величины вырезанных углов.
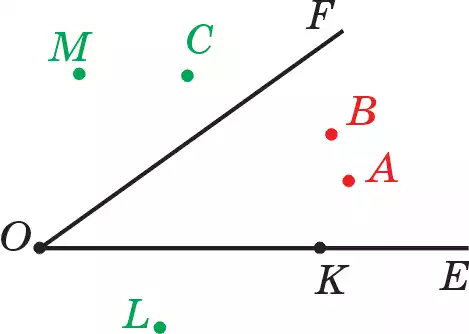
44. Даны лучи ОМ, ОN, ОL (рис. 38). Сколько на рисунке изображено углов? Напишите их.
45. Даны угол ЕОF и несколько точек (рис. 39). Назовите точки, лежащие: 1) внутри угла; 2) вне угла; 3) на сторонах угла.
46. Соединив каждые две точки, данные в задании 45, начертите отрезки АВ, ВС, СМ, LК, АL. Какие из этих отрезков лежат: 1) внутри угла; 2) вне угла; 3) пересекают стороны угла ЕОF? Поясните ответ.
47. На прямой а обозначьте точки А,О,В так, чтобы точка О лежала между точками А и В. Какой угол образуют лучи ОА и ОВ? Запишите его.
48. Дан луч СО. Проведите луч ОD таким образом, чтобы он вместе с данным лучом образовал развернутый угол.
49. Дан развернутый ∠АОВ и проведен луч ОС. Какими будут ∠АОС и ∠СОВ, образованные лучом ОС? Какие могут быть ответы?
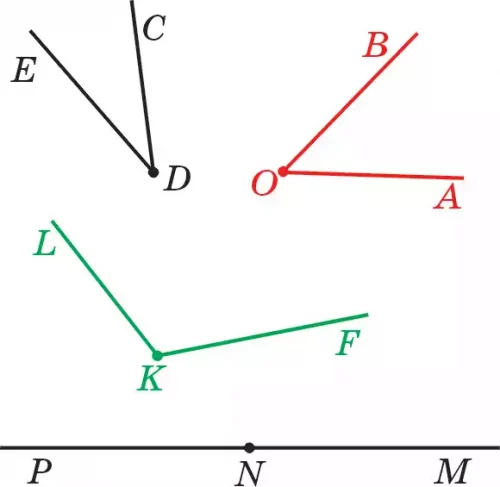
50. Прямые а и b пересекаются в точке О (рис. 40). 1) Сколько при этом образуется углов? 2) Запишите каждый из полученных углов. 3) Определите развернутые углы.
51. На рис. 41 изображены разные углы. 1) измерьте с помощью транспортира величины этих углов; 2) напишите их градусные меры; 3) определите виды этих углов.
52. Дан развернутый угол АОВ. Постройте прямой угол АОС, расположенный в одной полуплоскости относительно прямой АВ. 1) Докажите, что ∠СОВ = 90°. 2) В полуплоскости, содержащей луч ОС, начертите лучи ОD и DЕ так, чтобы угол АОD был острым, а угол АОЕ — тупым. 3) Измерьте углы АОD и АОЕ, сравните их с прямым углом. К какому выводу вы пришли?
53. Какие из углов: 1) 18°, 2) 92°, 3) 109°, 4) 90°, 5) 180° являются острыми, прямыми, тупыми, развернутыми?
54. Даны углы АОВ = 42°, ВОС = 28°. Найдите градусную меру угла АОС.
55. Если ∠АОС = 104°, ∠АОВ = 80° (из задания 54), то чему равен угол ВОС?
56. ОС — биссектриса ∠АОВ= 70°. Найдите градусную меру углов АОС и СОВ, сравните их.
57. Дан угол АОВ. Проведите луч ОС так, чтобы выполнялось равенство ∠АОС +∠СОВ =∠АОВ, если ∠АОВ: 1) развернутый; 2) неразвернутый. В какой полуплоскости относительно луча ОА и его дополнения расположен луч ОС? Сколько таких лучей можно провести?
58. Выполните действия, результат изобразите на рисунке: 1) 30° + 45°; 2) 120° – 30°; 3) 11° · 4; 4) 60° · 2.
59. 1) Даны углы: 2°; 15°; 1,5°; 8° 17′. Выразите их градусные меры в минутах. 2) Выразите в градусах: 240′; 30′; 360′.
60. Какую часть 1) прямого угла; 2) развернутого угла составляет угол, равный: 30°; 45°; 60°; 15°?
61. Сколько градусов составит угол, равный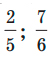
части: 1) прямого угла; 2) развернутого угла?
62. 1) ∠АОВ= 20°;∠ВОС= 50°, найдите ∠АОС. Какой луч расположен между двумя другими? 2) ∠АОС = 60°; ∠ВОС=35°, вычислите ∠АОВ. Рассмотрите все случаи.
63. Отметьте точку С, принадлежащую прямой АВ. Через точку С проведем луч СD так, чтобы ∠АСD был в 4 раза больше ∠ВСD. Найдите эти углы.
64. Угол АВС в сумме с данным углом равен двум прямым углам. Начертите их.
65. Поставьте вместо звездочек знак “ < ” или “ > ” (рис. 42): 1) ∠АОD*∠АОС; 2) ∠АОЕ*∠АОВ;
3) ∠ВОС*∠BOD.
66. Сколько углов, которые не являются развернутыми, образуется при пересечении двух прямых?
