БҰРЫШ. БҰРЫШТЫҢ БИССЕКТРИСАСЫ

Бұрыштың анықтамасы

Жазықтықты сәуле және түзудің көмегімен бөліктерге бөлу түсініктерін пайдаланып, бұрышты анықтауға болады.
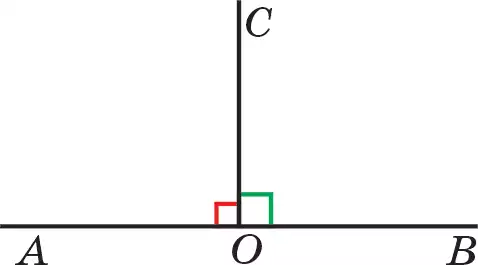
А н ы қ т а м а. Бір нүктеден шыгатын екі сәулемен шектелген жазықтықтың бөлігі бұрыш деп аталады.
Сәулелер бұрыштың қабыргалары, ал олардың бас нүктесі бұрыштың төбесі деп аталады. Бұрышты “∠”  таңбасымен және қабырғалары мен төбесіне жазылған әріптермен белгілейді.
Төбесі белгіленген әріп басқа екі әріптің ортасында жазылады. Мысалы, 29.1-суретте ∠АОВ немесе ∠ВОА (АОВ немесе ВОА бұрышы) кескінделген. Бұрышты жалғыз әріппен — оның төбесінің атауы-мен немесе қандай да бір санмен белгілеуге де болады (∠С, ∠ I, 29.2,3-суреттер).
Екі сәуле жазықтықты екі бөлікке бөліп тұр. Жазықтықтың қарастырылып отырған бөлігі суретте доғамен көрсетіледі.

Бұрыштардың теңдігі

Енді бұрыштардың теңдігін қарастырайық.
А н ы қ т а м а. Екі бұрышты беттестіргенде сәйкес қабырғалары және төбелері дәл келсе, олар тең бұрыштар деп аталады.
Мысалы, 30.1-суретте бейнеленген АВС және DЕҒ бұрыштары тең: ∠АВС = ∠DЕҒ. Себебі В төбесін Е төбесіне, ВА қабырғасын ЕD қабырғасына дәл келтіргенде, ВС және ЕҒ қабырғалары да дәл келеді.
ЕD сәулесіне толықтауыш ЕL сәулесін сызайық (30.2-сурет). Сонда ЕҒ сәулесі DL түзуімен бөлінген жарты жазықтықтардың бірінде, мысалы, α1 жарты жазықтығында жатады.

АВС бұрышының В төбесін DЕҒ бұрышының Е төбесіне, ВА қабырғасы мен ЕD қабырғасын беттестіргенде ВС мен ЕҒ қабырғалары дәл келмесе екі түрлі жағдай болуы мүмкін (31-сурет). Біріншісі, DЕҒ бұрышының ЕҒ қабырғасы АВС бұрышының ВА мен ВС қабырғаларының арасынан өтеді (31.1-сурет), яғни ∠АВС > ∠DЕҒ.
Бұл жағдайда ∠АВС = ∠АВҒ + ∠ҒВС екенін көру қиын емес.
Екіншісі, АВС бұрышының ВС қабырғасы DЕҒ бұрышының ЕD мен ЕҒ қабырғаларының арасынан өтеді. Онда ∠АВС < ∠DЕҒ (31.2-сурет). Бұл жағдайда, ∠АВС = ∠АВҒ — ∠ҒВС. Ендеше, АВС бұрышына тең бұрышты түзу арқылы бөлінген жарты жазық-тықтардың біріне түзуде жатқан сәуледен бастап салуға болады. Демек, бұрыш берілсе, онда төбесі және бір қабырғасы жазықтықты бөліп тұрған түзуде жататын, ал екінші қабырғасы берілген жарты жазықтықта жататын етіп берілген бұрышқа тең бұрышты әрдайым салуға болады.
Ортақ ОҒ қабырғасы бар РОҒ және ҒОN бүрыштары тең болса, онда ОҒ сәулесі РОN бұрышын қақ бөледі (32-сурет).

Анықтамалар. Бұрыштардың түрлері

А н ы қ т а м а. Бұрыштың төбесінен шығып, оны қақ бөлетін сәуле осы бұрыштың биссектрисасы деп аталады.
Енді бұрыштардың түрлеріне тоқталайық.
А н ы қ т а м а. Қабырғалары толықтауыш сәулелер болатын бұрыш жазыңқы бұрыш деп аталады.
33-суретте көрсетілген ∠DОС — жазыңқы бұрыш. АОВ жазыңқы бұрыш берілсін (34-сурет). Бұл бұрышты тең екіге бөлетін, яғни ∠ВОС = ∠СОА болатын етіп, ОС сәулесін жүргізейік.
А н ы қ т а м а. Жазыңқы бұрыштың жартысы тік бұрыш деп аталады.
ВОС және АОС бұрыштарының әрқайсысы тік бұрыш (34-сурет).
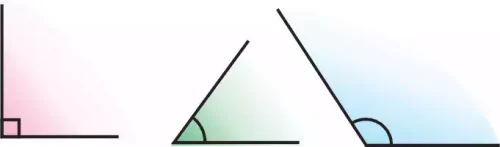
А н ы қ т а м а. Тік бұрыштан кіші бұрыш сүйір бұрыш деп аталады.
А н ы қ т а м а. Тік бұрыштан үлкен, жазыңқы бұрыштан кіші бұрыш доғал бұрыш деп аталады.
Сонымен біз бұрыштардың төрт түрін қарастырдық: сүйір бұрыш, тік бұрыш, доғал бұрыш, жазыңқы бұрыш (33-, 35-суреттер),

Бұрыштарды өлшеу

Енді бұрышты өлшеуге тоқталамыз, Бұрышты өлшеумен сендер 5-сынып математикасынан қысқаша таныссыңдар,
Бұрыштың шамасын өлшеу үшін бұрыштың өлшем бірлігін таңдап алу керек, Біз жоғарыда бұрыштарды тік бұрышпен салыс-тырдық, Сондықтан өлшеуді осы бұрышпен салыстырып жүргізген ыңғайлы, Тік бұрышты тең 90 бөлікке бөліп оның бір бөлігін, басқаша
айтқанда, тік бұрыштың бөлігін 1 градус деп атайды, Ол 1° деп белгіленіп, бұрышты өлшеудің бірлігі ретінде қабылданады,
Бұрыштың басқа да өлшем бірліктері бар, олар минут (‘), секунд («), яғни 1° = 60‘, 1’ = 60», Тік бүрыш 90 градусқа тең, Оны 90° деп жазамыз, Ал жазыңқы бұрыш тік бұрыштан екі есе үлкен бол-ғандықтан, ол 180°-қа тең.
Сүйір бұрыштың немесе доғал бұрыштың градустық өлшемін білу үшін оларды өлшеу керек.
Бүрыштарды өлшеу үшін арнайы құрал — транспортир қол-данылады.
36-суретте транспортирдің көмегімен 30°-қа, 90°-қа, 120°-қа тең бұрыштарды өлшеу жолы көрсетілген. Өлшеу нәтижесін былай жазамыз: ∠ВОС = 30°, ∠ВОD= 90°, ∠ВОА = 120°.
ВОА бұрышы ВОD және DОА бұрыштарының қосындысынан тұрса (36-сурет), яғни ∠ВОА = ∠ВОD + ∠DОА болса, онда ВОD және DOА бұрыштарының градустық өлшемдерінің қосындысы ВОА бүрышының градустық өлшеміне тең, шынында ∠ВОD = 90°, ∠DОА = 30° болса, ∠ВОА = ∠ВОD + ∠DОА = 90° + 30° = 120°. Мұндағы ОD сәулесі ВОА бұрышының қабырғаларының арасынан өтіп тұр, онда ∠СОА = ∠ВОА — ∠ВОС = 120° — 30° = 90°. Екі бұрыштың градустық өлшемдері тең болса, онда ол бұрыштар тең болады. Мұнда ∠ВОD = ∠СОА = 90°.

Енді бұрыштарды олардың градустық өлшемдері бойынша да сипаттай аламыз.
Атап айтсақ, сүйір бұрыштың өлшемі 0°-тан үлкен, бірақ 90°-тан кіші, ал доғал бұрыштың өлшемі 90°-тан үлкен, бірақ 180°-тан кіші болады.
Транспортирдің көмегімен бұрыштық өлшемі белгілі бұрышты салуға болады. Мысалы, 37-суретте бұрыштық өлшемі 60°-қа тең КОD бұрышын салу жолы көрсетілген.

Аксиомалар. Бұрыштар

Сонымен бұрыштардың теңдігінен, оларды өлшеудің негізінде бұрыштарды өлшеудің негізгі қасиеттері шығады. Олар III топтың аксиомаларына кіреді.
Ш₃. Әрбір бұрыштың нөлден үлкен белгілі бір градустың өлшемі бар болады.
Ш₄. Егер сәуле бұрыштың төбесінен шығып, оның қабырғаларының арасында жатса, онда берілген бұрыш пайда болган бұрыштардың қосындысына тең.
Жоғарыда ұзындықтары берілген кесінділерді сөуленің бойына, оның бас нүктесінен бастап өлшеп салуға болатынын айттық.
Осы сияқты бұрыштың өлшем бірлігі берілген жағдайда, берілген жарты жазықтықта берілген сөуледен бастап транспортирді туралап қойып, бұрыштың градустық өлшемін таптық. Берілген бұрышқа тең бұрышты салу мүмкін екенін көрдік. Осы түсініктердің негізінде кесінділерді жөне бұрыштарды өлшеп салудың негізгі қасиеттерін баяндауға болады. Ол төртінші топтың аксиомаларын құрайды.
ІV₁. Қандай сәуле болса да, оның бойына бас нуктесінен бастап узындығы берілген кесіндіні бір ғана жолмен өлшеп салуға болады.
ІV₂. Градустың өлшемі 180°-тан кіші болатын бұрышты, берілген жарты жазықтықта берілген сәуледен бастап бір ғана жолмен салуға болады.

Сұрақтар

1. Екі сүйір бұрыштың қосындысы 180°-қа тең немесе артық болуы мүмкін бе? Жауабын түсіндіріңдер.
2. Кесінді мен бұрыштың салынуындағы ұқсастық пен айырмашылық неде?

Жаттығулар

43.Түрлі түсті қағазға сүйір, тік, доғал бұрыштар сызып, қиып алыңдар, оларды салыстырыңдар. Қиып алған бұрыштардың шамаларын транспортирді пайдаланып анықтаңдар.
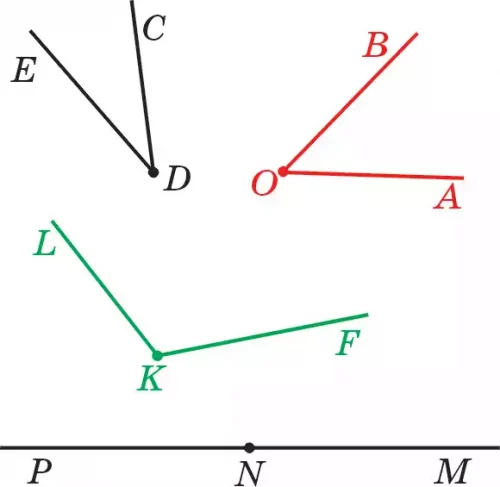
44. ОМ, ОN, ОL сәулелері берілген (38-сурет). Суретте неше бұрыш бар? Әрқайсысын белгілеп жазыңдар.
45. ЕОҒ бұрышы жөне бірнеше нүктелер берілген (39-сурет). Бұл бұрыштың 1) ішінде; 2) сыртында; 3) қабырғаларында жатқан нүктелерді атаңдар.

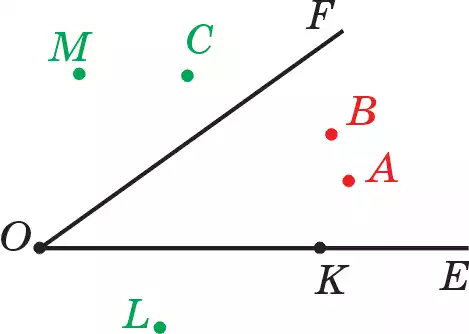
46. 45-есепте берілген өрбір екі нүктені қосып АВ, ВС, СМ, LК, АL кесінділерін сызыңдар, ЕОҒ бұрышының 1) ішінде жатқан; 2) сыртында жатқан;
3) қабырғаларды қиып өткен кесінділерді анықтаңдар. Жауапты түсіндіріңдер.
47. а түзуінен А, О, В нүктелерін белгілеңдер. О нүктесі А мен В нүктелерінің арасында жатсын. ОА, ОВ сөулелері қандай бұрыш құрайды? Оны белгілеп жазыңдар.
48. ОС сәулесі берілген. Осы сәулемен жазыңқы бұрыш жасайтын О^ сәулесін жүргізіңдер.
49. АОВ жазыңқы бұрышы берілген және ОС сәулесі жүргізілген. Пайда болған АОС және СОВ бұрыштары қандай бұрыштар болады?
50. а және b түзулері О нүктесінде қиылысады (40-сурет). 1) Неше бұрыш пайда болды? 2) Әрбір бұрышты белгілеп жазыңдар. 3) Жазыңқы бұрышты анықтаңдар.
51. 41- суретте әртүрлі бұрыштар көрсетілген. 1) Бұрыштарды транспортирдің көмегімен өлшеңдер. 2) Градустық өлшемдерін жазыңдар. 3) Бұрыштардың қайсысы сүйір, тік, доғал және жазыңқы болатынын анықтаңдар.
52. АОВ жазыңқы бұрыш берілген. АВ түзуімен анықталған жарты жазықтықтың біріндегі АОС тік бұрышын салыңдар. 1) ∠СОВ = 90° болатынын дәлелдеңдер.
2) ОС сәулесі жатқан жарты жазықтықта ∠АОD сүйір, ∠АОЕ доғал бұрыш болатын етіп ОD, ОЕ сәулелерін сызыңдар. 3) АОD, АОЕ бұрыштарын өлшеп, оларды тік бұрыштармен салыстырыңдар. Қаңдай қорытынды бере аласыңдар?
53. 1) 18°; 2) 92°; 3) 109°; 4) 90°; 5) 180° бұрыштары берілген. Осы бұрыштардың қайсысы сүйір, тік, доғал және жазыңқы бұрыш болады?
54. ∠АОВ = 42°, ∠ВОС = 28° және олар тек бір қабырғасына ортақ бұрыштар болсын. АОС бұрышының шамасын табыңдар.

55.54-есептегі ∠АОС = 104°, ∠АОВ = 80° болса, ∠ВОС бұрышы неге тең?
56. ∠АОВ = 70° болатын бұрышқа ОС биссектрисасы жүргізілген. АОС және СОВ бұрыштарын анықтап, салыстырыңдар.
57. АОВ бұрышы берілген. Егер АОВ бұрышы 1) жазыңқы; 2) жа-зыңқы емес болса, ∠АОС + ∠СОВ = ∠АОВ болатын ОС сәулесін жүргізіңдер. ОС сәулесі ОА сәулесіне және оның толықтауышына қарағанда қандай жарты жазықтықта жатады? Ондай саулелердің нешеуін жүргізуге болады?
58. Амалдарды орындап, нәтижелерін сызбада көрсетіңдер: 1) 30° + 45°; 2) 120° — 30°; 3) 11° • 4; 4) 60° • 2.
59. 1) 2°; 15°; 1,5°; 8°17’ бұрыштары берілген. Оларды минуттар арқылы жазыңдар. 2) 240’; 30’; 360’ бұрыштарының әрқайсысын градус арқылы жазыңдар.
60. 30°; 45°; 60°; 15° бұрыштарының әрқайсысы 1) тік бұрыштың; 2) жазыңқы бұрыштардың қандай бөлігін құрайды?
61. 1) Тік бұрыштың; 2) жазыңқы бұрыштың

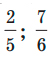
бөлігі неше градустық бұрыш болады?