Теорема
Сумму внутренних углов любого треугольника можно найти на основе следующей теоремы.
Теорема. Сумма внутренних углов треугольника равна 180°.
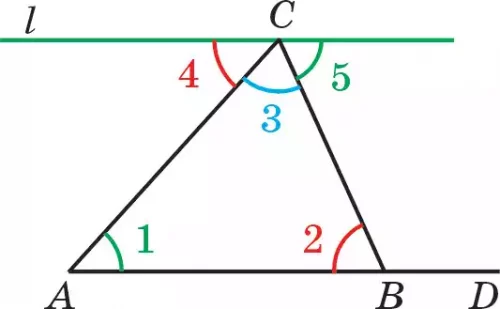
Доказательство. Пусть дан ΔАВС (рис. 87). Его внутренними углами являются ∠1, ∠2, ∠3. Через вершину С проводим прямую l параллельно стороне АВ. На основании аксиомы V прямая l будет единственной.
Сторона АС является секущей двух параллельных прямых l и АВ, при этом образуются внутренние накрест лежащие углы: ∠1= ∠4 и ∠2 = ∠5 (признак параллельности прямых).
Известно, что ∠4 + ∠3 + ∠5 = 180° (развернутый угол). Тогда ∠1 + ∠2 + ∠3 = 180°. Теорема доказана.
Определение
Определение. Угол, смежный с внутренним углом треугольника, называется его внешним углом.
На рис. 87 изображен ΔАВС, смежным углом его внутреннему ∠2 будет ∠DВС. Поэтому ∠DВС является внешним углом треугольника.
Следствия
Следствия из теоремы о сумме внутренних углов треугольника.
1. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. На основании теоремы о сумме внутренних углов треугольника:
∠1 + ∠3 + ∠2 = 180° или ∠1 + ∠3 = ∠180° – ∠2. ∠DВС — внешний угол: ∠DВС + ∠2 =∠180°, отсюда ∠DВС = ∠180° – ∠2. Из равенства (1) и (2) имеем:
∠DВС = ∠1 + ∠3. Следствие 1 доказано.
2. У треугольника не может быть больше одного тупого (прямого) угла. Значит, у тупоугольного (прямоугольного) треугольника имеются два острых угла.
3. Сумма острых углов прямоугольного треугольника равна 90°. Пусть в ΔАВС ∠С = 90°. Тогда ∠А и ∠В будут острыми. На основании теоремы о сумме внутренних углов треугольника ∠А + ∠С+ ∠В=180° или ∠А + ∠90° + ∠В = 180°, отсюда следует, что ∠А + ∠В = 90°.
4. Если два угла одного треугольника равны соответствующим двум углам другого треугольника, то равны и их третьи углы.
Пусть даны ΔАВС и ΔА′В′С′ и ∠А = ∠А′, ∠В = ∠В′. На основании теоремы о сумме внутренних углов треугольника: ∠А+ ∠В+ ∠С= 180°, отсюда имеем, ∠С = 180° – ∠A – ∠B или ∠С =180° – ∠А′ – ∠В′. (1) ∠А′ + ∠В′+∠С′ = 180°, отсюда ∠С′ =180° – ∠А – ∠B. (2) Из равенств (1) и (2) имеем: ∠С = ∠С′.
Следовательно, если два прямоугольных треугольника имеют по одному равному острому углу, то у них равны и вторые острые углы.
Примеры
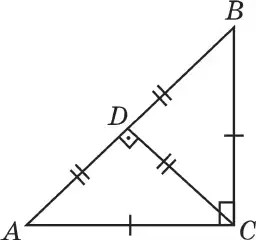
Пример 1. Доказать, что длина перпендикуляра пущенного из прямого угла к гипотенузе
прямоугольного треугольника с острым углом 45°, равна половине гипотенузы (Рис.88).
Р е ш е н и е . Пусть в треугольнике АВС: ∠С = 90°, ∠А = 45°. На основании теоремы о сумме
углов треугольника: ∠В+45°+90°=180°, ∠В= 45°. Значит ΔАВС-равнобедренный:АС = ВС. Проведем высоту СD,тогда каждый из прямоугольных треугольников АDС, ВDС — равнобедренный.
Отсюда DС = АD =ВD.
Пример 2. Равнобедрнный ΔАВС с основанием АВ с помощью отрезка АD разделен на два равнобедренных треугольника: ΔАСD и ΔАВD с основаниями соответственно АС и ВD. Найдите углы ΔАВС.
Р е ш е н и е . Из условия задачи имеем следующее: ΔАВС — равнобедренный, АВ — его основание. Отрезок АD разбивает ΔАВС на два равнобедренных треугольника (рис.89)
Требуется найти углы ∠А, ∠B и ∠С. По свойству равнобедренного треугольника: АС
= ВС; ∠А=∠B.
По теореме о сумме углов треугольника ∠А+∠B+ ∠С = 180°. В ΔАСD: ∠1=∠2, а в ΔАВD: ∠4=∠5.
По условию ∠2+∠3=∠4. ∠5 — внешний угол треугольника АСD, тогда ∠5=∠1+∠2=∠1+∠1=2 · ∠1.
На основании теоремы о сумме углов треугольника имеем: ∠1+∠2+∠3+∠4=180°. ∠1+2 ∠4=180°, так как ∠4=∠5=2 · ∠1. Значит, ∠1+2 · 2 · ∠1= 180°, 5 · ∠1=180°, ∠1=180/5 =36 · ∠4 = 2 · 36° = 72°.
Ответ: ∠А = ∠B = 72; ∠С = 36°.

Вопросы
1. Какие знания были использованы при доказательстве теоремы о сумме внутренних углов треугольника?
2. Может ли сумма величин острых углов тупоугольного треугольника быть равной 90°? Ответ обоснуйте.
3. У всех ли треугольников каждая высота проходит внутри треугольника? Ответ обоснуйте.
Упражнения
180. Существуют ли треугольники с углами: 1) 45°, 35°, 110°; 2) 70°, 60°, 50°; 3) 90°, 60°, 45°; 4) 55°, 45°, 60°?
181. Найдите третий угол треугольника по двум данным углам: 1) 30°, 50°; 2) 60°, 40°; 3) 29°, 30°; 4) 81°, 90°.
182. Один внешний угол треугольника составляет 2/3, а внутренний угол —4/9 (внутренних) суммы его углов. Найдите все углы треугольника.
183. Один угол треугольника на 45° больше второго, а третий на 15° меньше второго угла. Найдите углы треугольника.
184. В ΔАВС: ∠А + ∠В = 110° и ∠В + ∠С = 120°. Найдите углы треугольника.
185. Отношение углов треугольника равно 4 : 2 : 3. Найдите каждый его угол.
186. Отношение двух углов треугольника равно 5 : 7, а третий угол на 44° больше, чем меньший угол. Найдите третий угол треугольника.
187. В ΔАВС ∠А= 60°, ∠В= 30°, СD— высота, СЕ — биссектриса. Найдите ∠DСЕ.
188. В ΔDЕF ∠D = 76°, ∠F = 60°. Найдите угол между биссектрисами ∠D и ∠Е?
189. Внешние углы в двух вершинах треугольника равны 110° и 160°. Найдите каждый угол треугольника.
190. Два внешних угла треугольника 120° и 160°. Найдите его третий внешний угол. Сделайте вывод о сумме внешних углов треугольника.
191. Сумма внешних углов в вершинах В и С ΔАВС равна 250°. Найдите внутренний угол А треугольника.
192. Один из внутренних углов треугольника равен 50°, а один из внешних его углов равен 85°. Найдите остальные внутренние углы треугольника.
193. Докажите, что треугольник не имеет: а) двух тупых углов; б) двух прямых углов; в) тупого и прямого угла.
194. Внешний угол треугольника при вершине В в три раза больше его внутреннего угла А и на 40° больше внутреннего угла С. Найдите углы треугольника.
195. Один из углов треугольника равен 61°. Найдите острый угол, образованный между сторонами и биссектрисами его остальных углов.
196. Биссектрисы углов В и С ΔАВС пересекаются в точке О. ∠ ВАС равен половине ∠ВОС. Найдите ∠А.
197. Угол при вершине равнобедренного треугольника равен 75°. Найдите угол при основании.
198. Угол при основании равнобедренного треугольника равен 49°25′. Найдите угол при вершине.
199. Докажите, что каждый угол равностороннего треугольника равен 60°.
200. Угол при вершине равнобедренного треугольника равен 80°. Найдите угол между высотой, опущенной на боковую сторону, и основанием.
201. Угол при основании равнобедренного треугольника равен 50°. Найдите угол между одной боковой стороной и высотой, опущенной на другую боковую сторону.
202. Угол между высотой и боковой стороной равнобедренного треугольника на 15° меньше угла при его основании. Найдите углы треугольника.
203. Если соединить точки D, Е, F, являющиеся серединами сторон равностороннего ΔАВС, образуется новый треугольник. Докажите, что:
1) ΔАDF = ΔDВE. Перечислите равные треугольники; 2) DЕ || АС. Перечислите все параллельные стороны; 3) АЕ ⊥ ВС; 4) DЕ = 1/2 АС.
204. Докажите, что в равнобедренном треугольнике: 1) биссектрисы; 2) медианы, проведенные из вершин основания, равны.
205. Разность между двумя углами равнобедренного треугольника 24°. Найдите его углы.
206. В равнобедренном треугольнике: 1) угол при основании в 4 раза больше угла при вершине; 2) угол при вершине в 4 раза больше угла при основании.
Найдите углы треугольника.
207. В ΔАВС стороны АВ = 6 дм, ВС = 6 дм, СА = 9 дм. Ответьте: а) какой угол в треугольнике самый большой; б) какие его углы равны?