Теорема 1

Теорема 1. Если прямая перпендикулярна одной из параллельных, прямых, то она перпендикулярна и второй прямой.
Доказательство. Пусть даны прямые а, в, с такие, что а||в и с а (рис. 90). Прямая с секущая, поэтому, ∠1+ ∠2=180°, как сумма внутренних односторонних углов. ∠1=90°, поэтому и ∠2=90°.
Значит с в.
Теорема доказана.
Теорема 2
Теорема 2. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
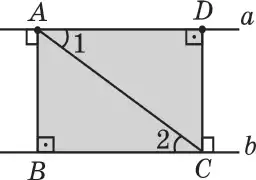
Доказательство. Рассмотрим параллельные прямые аи в . Отметим на прямой а точкуА и проведем из этой точки перпендикуляр АВ к прямой в (рис. 91). Докажем, что расстояние от любой точки D прямой а до прямой в равно АВ. Проведем из точки D перпендикуляр DС к прямой в . Так как DСв, то DСа (по теореме 1). Прямоугольные треугольники АВС и
DСА равны, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых а и в секущей АС. Следовательно, DС = АВ.
Итак, любая точка D прямой а находится на расстоянии АВ от прямой в. Все точки прямой в находятся на таком же расстоянии от прямой а. Теорема доказана.
Расстояние от произвольной точки одной из паралельных прямых до другой прямой называется расстоянием между этими прямыми.
Упражнения
208. Один из острых углов прямоугольного треугольника равен: 1) 18°; 2) 56°. Найдите его второй острый угол.
209. Один из острых углов прямоугольного треугольника равен 60°: 1) катет, прилежащий к этому углу, равен 6,5 см. Вычислите гипотенузу;
2) сумма меньшего катета и гипотенузы — 3,6 дм. Найдите длину гипотенузы и меньшего катета.
210. Гипотенуза прямоугольного треугольника равна 18 м, один из его острых углов — 30°. Найдите длину катета, лежащего против этого угла.
211. В ΔKLM отрезок КМ = 24,8 дм, ∠М=30°, ∠K = 90°. Найдите: 1) расстояние от точки К до прямой LM; 2) проекцию наклонной LМ на прямой КL.
212. В ΔDEF ∠D = ∠F = 45° и DF = 16,4 м. Найдите: 1) расстояние от точки Е до прямой DF; 2) проекцию наклонной DЕ на прямой DF.
213. Прямая, пересекая две параллельные прямые, образует угол 30°. Длина отрезка между параллельными прямыми 17,6 дм. Найдите расстояние между параллельными прямыми.
214. В равнобедренном ΔАВС боковая сторона равна 16,4 дм. Из точки D, являющейся серединой боковой стороны АВ, проведен перпендикуляр. Этот перпендикуляр пересекает сторону ВС в точке Е. Периметр ΔАЕС равен 26,9 дм. Найдите сторону АС.
215. Докажите, что прямая, перпендикулярная биссектрисе угла, пересекает стороны этого угла, начиная с вершины, на равные отрезки.
216. Один острый угол прямоугольного треугольника равен 45°: 1) один из катетов — 8 дм; найдите его второй катет; 2) сумма катетов — 28 дм; найдите каждый катет;
3) сумма гипотенузы и высоты, опущенной к ней, — 21 дм. Найдите гипотенузу и высоту.
217. Докажите, что если катет прямоугольного треугольника равен половине гипотенузы, то один из его углов равен 30°.
218. В ΔАВС медиана ВD равна половине стороны АC. Найдите ∠В.
219. Отношение углов треугольника равно отношению чисел 1, 2 и 3. Докажите, что он будет прямоугольным треугольником.
220. Докажите, что угол между биссектрисами острых углов прямоугольного треугольника равен 145°.
221.Докажите, что высоты, опущенные на стороны равностороннего треугольника будут равны.
222. Если высоты в треугольнике равны, то докажите, что такой треугольник равносторонний.
223. В равностороннем треугольнике проведены две медианы. Найдите острый угол между ними.
224. Один из острых углов прямоугольного треугольника равен 50°. Найдите угол между биссектрисой прямого угла и гипотенузой.