Определения
Среди замкнутых линий окружность является самой простой.
Определение. Множество точек плоскости, равноудаленных от данной точки, называется окружностью.
Данную точку (О) называют центром окружности. Для изображения окружности используется циркуль. На рис. 80 изображена окружность с центром в точке О. Точки А, В, С лежат на окружности. Видно, что ОА = ОВ = ОС.
Определение. Отрезок, соединяющий центр с какой -либо точкой окружности, называется радиусом окружности.
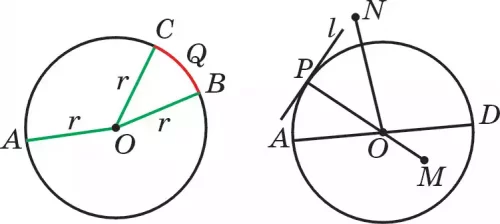
Радиус обозначают латинской буквой r или R , которая читается как “эр”. Тогда видно, что ОА = R. Окружность с центром в точке О и радиусом r обозначается как ω(О; r). Возьмем на окружности ω(О; r) любые две точки В и С (рис. 92.1). Эти точки делят окружность на две части. Каждая из этих частей называется дугой окружности или просто дугой. Точки В и С делят окружность на дуги ВQС и САВ. Q — любая точка окружности, лежащей между точками В и С, а точка А лежит между точками С и В. Дуги обозначаются ∪ВQС и ∪САВ или с помощью делящих точек: ∪ВС и ∪СВ (перед буквами ставится знак дуги — “∪”).
Точки М и N, изображенные на рис. 92.2, не лежат на окружности. Говорят, что точка М лежит внутри окружности, а точка N — вне окружности, потому что, согласно определению окружности, ОМ < r, а ОN > r.
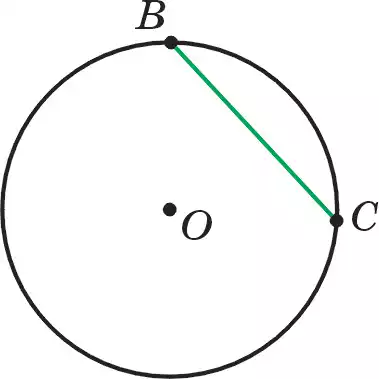
Определение. Отрезок, соединяющий две любые точки окружности, называется ее хордой(В переводе с греческого означает “струна”.).
Дуга ∪ВС, определенная через концы хорды ВС окружности, считается соответствующей этой хорде или опирающейся на эту хорду (рис. 92.3).
Определение. Хорда, проходящая через центр окружности, называется ее диаметром.
На рис. 92.2 АD — диаметр. АD=АО+ОD= 2r. Центр окружности является серединой диаметра. Дугу, опирающуюся на диаметр, называют полуокружностью.
Две окружности равны между собой, если равны их радиусы. При наложении их центров друг на друга равные окружности совпадут.
Окружность также можно определить как геометрическое место точек. Геометрическое место точек определяет какую-либо одну фигуру. При этом ставится определенное условие: все точки, принадлежащие геометрическому месту точек (фигуре), должны обладать одинаковым свойством. Геометрическому месту точек можно дать следующее определение.

Определение. Фигуру, состоящую из точек, обладающих определенным свойством, называют геометрическим местом точек.
Например, на плоскости геометрическим местом точек, равноудаленных от данной точки, будет
окружность.
Здесь за определение свойства геометрического места точек берется понятие равноудаленности. Пусть дана окружность (О; r) (рис. 93).
Определение. Угол, образованный двумя радиусами окружности, называется центральным углом.
Угол ВОС, расположенный между радиусами ОВ и ОС, является центральным углом. Стороны центрального угла делят окружность на две дуги. Одна из них ВС лежит внутри центрального
угла ВОС, поэтому эта дуга является соответствующей центральному углу.
Итак, дуга ВС называется соответствующей центральному углу ВОС. И, обратно, дуге ВС соответствует центральный угол ВОС. Считается, что градусная мера дуги равна градусной мере центрального угла. Например: если ∪ВОС = 48°, то ∪ВС = 48°. Отсюда: ∠ВОС = ∪ВС.
Значит, градусная мера полной окружности равна 360°, так как полный центральный угол окружности равен 360°. Проведем в окружности радиус ОD, тогда ∠DОВ + ∠ВОС= ∠DОС. Следовательно, можно сказать, что ∪DВ + ∪ВС = ∪DС. Значит, дуга, соответствующая центральному углу, равному сумме двух центральных углов, равна сумме дуг, соответствующих этим центральным углам.
Теорема

Теорема. Если равны два центральных угла окружности, то равны и соответствующие им дуги.
Доказательство. Дана окружность ω (О; r) (рис. 82). Пусть ∠АОВ, ∠СОD — центральные углы. Тогда ∪АВ, ∪СD — соответствующие им дуги. По условию теоремы ∠АОВ = ∠СОD, значит, лучи ОА, ОВ можно наложить на лучи ОС и ОD так, чтобы они совпали. Тогда точка А совпадет с точкой С, а точка В совпадет с точкой D, так как ОА=ОС, ОВ = ОD (как радиусы одной окружности).
Точно так же каждая из точек дуг АВ и СD лежит на одинаковом расстоянии от центра О. Поэтому при наложении дуга АВ совпадает с дугой СD, а по определению равенства фигур
∪АВ = ∪СD. Теорема доказана.
Сформулируйте и докажите теорему, обратную данной.
Вопросы
1. Какие известные вам понятия использованы в определении окружности?
2. Справедливо ли утверждение о том, что угол, образованный двумя лучами, исходящими из центра окружности, измеряется дугой, заключенной между этими лучами?
Упражнения

225. Можно ли назвать окружность геометрическим местом точек? Почему?
226. Начертите окружность с центром в точке О и радиусом r= 3,5 см. Проведите диаметр и радиусы разноцветными карандашами.
227. Начертите окружность с центром в точке С и диаметром АВ = 8 см. Проведите диаметр и радиусы разноцветными карандашами.
228. Начертите окружность (О; R) (рис. 95). Какие из данных точек А, В, D, Е, F, О лежат: 1) внутри окружности; 2) вне окружности; 3) на окружности. Можно ли сказать, что точка О лежит на окружности?
229. Если через точку А (рис. 83) провести прямую, то пересечется ли она с окружностью? Если пересечется, то сколько будет точек пересечения?
230. Пересекает ли окружность луч с началом в центре окружности (О, R)? Если пересекает, то сколько будет точек пересечения?
231. Начертите две пересекающиеся окружности ω(О, R) и ω1(О1, R1). Сколько точек пересечения может быть? Могут ли эти две окружности пересекаться в трех точках?
232. Начертите две окружности с общим центром и радиусами 2 см, 3 см. Какая из окружностей расположена внутри другой?
233. Начертите окружность ω(О; r). Отметьте на окружности точки С и D. Постройте центральный угол, соответствующий дуге ∪СD. Обозначьте его.
234. Найдите градусную меру центрального угла, соответствующего: 1) половине окружности; 2) 1/6 окружности.
235. Найдите угловую меру дуг ∪АВ, ∪ВС и ∪АС, если градусные меры соответствующих им центральных углов равны: ∠АОВ = 45°, ∠ВОС = 60°.
236. Докажите равенство центральных углов, соответствующих дугам ∪АВ и ∪СD окружности (О; R), если ∪АВ = ∪СD.
237. Полуокружность разделена на: 1) 3; 2) 4; 3) 6; 4) 18 равных частей. Найдите градусную меру каждой дуги и центрального угла, соответствующего этой дуге.