Смежные углы
Каждый из лучей, исходящих из вершины развернутого угла и не совпадающих с его сторонами, считается лежащим внутри развернутого угла. На рис. 43 луч ОD расположен внутри развернутого угла АОВ. В этом случае углы ВОD и АОD называются смежными.

Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
На рис. 43 ∠ВОD и ∠АОD смежные, у них сторона ОD общая, а стороны ОВ и ОА — дополнительные лучи.
Теорема. Сумма смежных углов равна 180°.
Доказательство. На основе аксиомы III4: ∠АОD + ∠DОB =∠AОB. ∠AОB — развернутый. Следовательно, ∠АОD + ∠DОB = 180°.
Теорема доказана.
Вертикальные углы
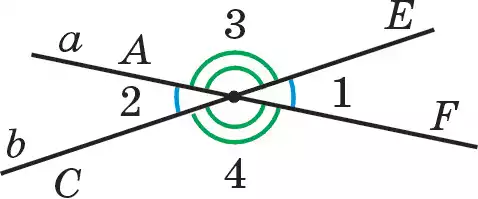
Пусть даны прямые а и b, пересекающиеся в точке О. Тогда на прямой а можно обозначить лучи ОА и ОF, а на прямой b — лучи ОС и ОЕ. При этом лучи ОF и ОЕ образуют ∠1, лучи ОА и ОС образуют ∠2; лучи ОЕ и ОА образуют ∠3; лучи ОС и ОF образуют ∠4. ∠1 и ∠2, ∠3 и ∠4 называют вертикальными углами.
Определение. Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
На рис. 44 лучи ОF и ОА, ОС и ОЕ являются попарно дополнительными лучами.
Теорема. Вертикальные углы равны.
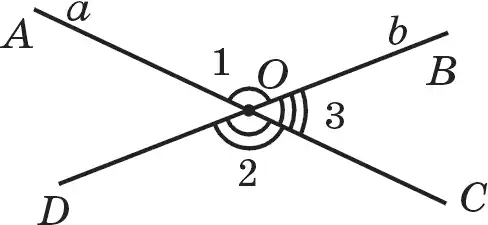
Доказательство. Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О (рис. 45). ∠1 и ∠2 — вертикальные углы.
∠АОС — развернутый, значит ∠АОС =180°. Однако ∠1 + ∠3= ∠АОС, т. е. ∠3 + ∠1 = 180°, отсюда имеем:
∠1=180°–∠3. (1)
Также имеем, что ∠DОВ = 180°, отсюда ∠2 + ∠3 = 180°, или
∠2 = 180°– ∠3. (2)
Так как в равенствах (1) и (2) правые части равны, то ∠1=∠2.
Теорема доказана.
Задание
Попытайтесь сформулировать теоремы о смежных и вертикальных углах, выделяя их условия и заключения.
Вопросы
1. Чем отличаются смежные и вертикальные углы? 2. Какие знания использованы при доказательстве теоремы о вертикальных углах?
Упражнения
75. Начертите острый угол. Дополните его до развернутого угла. Запишите полученные углы.
76. Даны смежные углы АВС и СВЕ. Найдите угол АВЕ. Сравните углы АВЕ и АВС.
77. Один из смежных углов равен: 1) 45°; 2) 120°; 3) 18°. Найдите второй угол.
78. Докажите, что если смежные углы равны, то они прямые.
79. Один из углов, образованных при пересечении двух прямых, равен 50°. Найдите остальные углы. Запишите смежные, развернутые углы.
80. Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
81. Докажите, что угол между биссектрисами смежных углов равен 90°.
82. Один из смежных углов в 5 раз больше другого. Найдите больший из них.
83. Найдите смежные углы, если один из них на 40° меньше другого.
84. Если один из смежных углов равен 48°, то найдите градусную меру второго угла.
85. Вычислите градусную меру каждого из смежных углов, если один из них:
1) больше на 64°; 3) в 3 раза больше; 2) больше на 56°; 4) в 2 раза меньше второго.
86. Найдите градусную меру двух углов, образованных при пересечении двух прямых, если:
1) сумма углов равна 70°; 2) один угол больше другого в 3 раза; 3) один угол на 35° меньше другого.
87. Дана точка С, принадлежащая прямой АВ. Через точку С проведем луч СD так, чтобы АСD был в 4 раза больше ВСD. Найдите эти углы.