Взаимное расположение прямой и окружности. Определение
Рассмотрим взаимное расположение прямой и окружности.
Возможны следующие три случая взаимного расположения прямой и окружности.
1. Прямая не имеет с окружностью ни одной общей точки (рис. 96.1).
2. Прямая с окружностью имеет только одну общую точку (рис. 96.2).
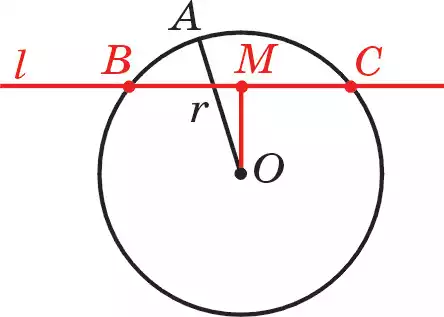
3. Прямая имеет с окружностью две общие точки (рис. 96.3).
Определение. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.
Теоремы 1 и 2
Определение. Прямая, имеющая с окружностью две общие точки, называется секущей.
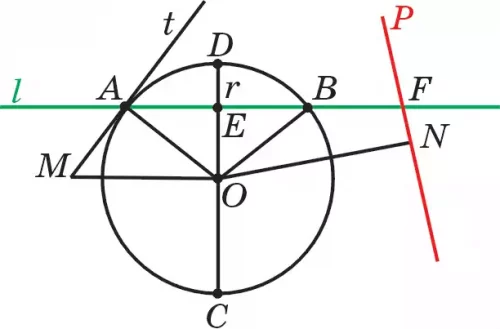
Пусть прямая l пересекает окружность (О; r) в точках А и В (рис. 97) и отрезок АВ будет хордой
окружности.
Теорема 1. Диаметр окружности, разделяющий хорду пополам, перпендикулярен этой хорде.
Доказательство. Допустим, диаметр СD в точке Е делит хорду АВ на две равные части: АЕ = ЕВ (рис. 97). По третьему признаку равенства треугольников ΔОАЕ = ΔОВЕ, откуда вытекает, что ∠ОЕА= ∠ОЕВ = 90°. Значит, ОЕ ⊥ АВ или СD ⊥ ОВ. Теорема доказана.
Теорема 2 (теорема, обратная теореме 1). Если диаметр окружности перпендикулярен хорде, то он разделит хорду на две равные части.
Докажите эту теорему самостоятельно.
Длина отрезка ОЕ определяет расстояние от центра О окружности до ее хорды АВ или до прямой l (рис. 85). Это расстояние обозначается через d, d = ОЕ. В ΔАОЕ : ОЕ < r или d < r.
Следствие 1. Если расстояние от центра окружности до секущей прямой меньше радиуса окружности, тогда прямая пересекается с окружностью в двух точках.
Следствие 2. Хорды окружности, находящиеся на одинаковом расстоянии от центра, равны. Справедливость этого следствия легко можно доказать, используя признаки равенства прямоугольных треугольников.
Теорема 3
Теорема 3. Касательная перпендикулярна радиусу, проведенному в точку касания.
Доказательство. Воспользуемся рис. 97. Пусть касательная, проходящая через точку А окружности, будет прямая t. Докажем, что ОА ⊥ t. Известно, что ОА = r. По определению касательной окружности касательная t имеет с окружностью ω только одну общую точку (точку касания). Все точки прямой t, кроме точки А, лежат вне окружности. Другими словами, для любой точки М прямой t (кроме точки А) ОМ>r. Тогда ОА = r будет расстояние от центра О до прямой t (до касательной). Значит, ОА ⊥ t. Теорема доказана.
Следствие 1. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной.
Это вытекает из теоремы 3.
Следствие 2. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не пересекается с окружностью.
Действительно, если расстояние ON от центра окружности О до прямой Р (рис. 85) будет больше радиуса r (d = ON > r), тогда каждая точка прямой Р от центра О лежит на расстоянии больше радиуса. Значит, каждая точка прямой Р лежит вне окружности, т. е. окружность не пересекается с прямой Р. Итак, если расстояние от центра данной окружности до прямой меньше (больше, равно) радиуса окружности, то прямая пересекает окружность в двух точках (не пересекает, касается).
Самостоятельная работа
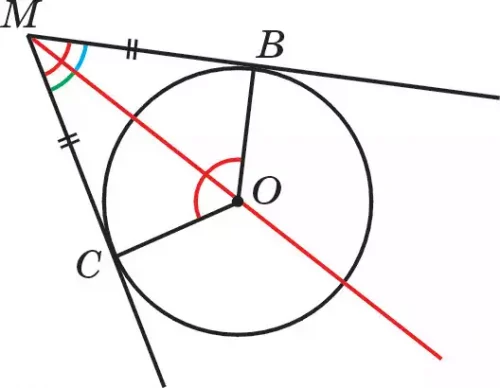
Используя рис. 98, попытайтесь самостоятельно объяснить и доказать справедливость следующих четырех утверждений:
Если из точки М, лежащей вне окружности, провести две касательные МВ и МС, то:
а) центр окружности лежит на биссектрисе ∠ВМС(О ∈ ОМ);
б) расстояния от вершины угла ВМС до точек касания равны (МВ = МС);
в) отрезки, соединяющие точки касания с центром окружности, являются ее радиусами и перпендикулярны сторонам угла ВМС (ОВ= = ОС = R, ОВ ⊥ ВМ, ОС ⊥ СМ);
г) ∠ВМС + ∠ВОС = 180°.
Взаимное расположение двух окружностей
Теперь рассмотрим взаимное расположение двух окружностей.
Пусть даны окружности ω(О; R) и ω′(О′; R′), расстояние между центрами окружностей d = ОО′. Для определенности будем считать, что R>R′.
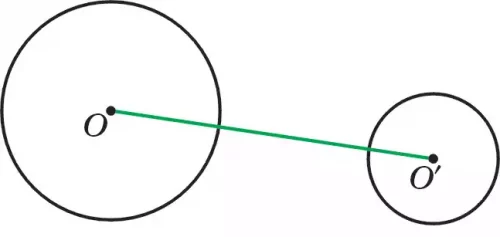
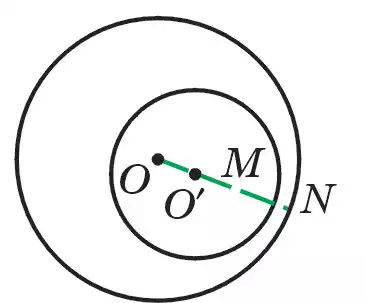
Рисунок 99
Взаимное расположение двух окружностей связано с расстоянием между их центрами. Здесь возможны следующие случаи.
1) Если R + R′ < d и d< R – R′ (рис. 99), тогда окружности не пересекаются.
2) Если R + R′ =d или R – R′ = d, тогда окружности будут иметь общую точку (касаются), лежащую на прямой, проходящей через центры окружностей (рис. 100).
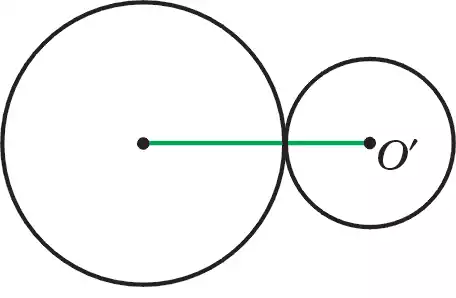

Рисунок 100
3) Если R + R′ > d или d > R – R′, тогда окружности пересекаются в двух точках (рис. 101).
Окружности, имеющие общий центр, называются концентрическими. При равных радиусах они совмещаются, при различных радиусах не имеют ни одной общей точки (рис. 102).

Вопросы
1. Как можно описать три возможных случая взаимного расположения прямой и окружности относительно радиуса с использованием понятия расстояния от точки до прямой?
2. К какому из перечисленных трех случаев взаимного расположения двух окружностей относятся концентрические окружности?
Упражнения
238. Начертите окружность ω (О; r). Сколько точек пересечения этой окружности: 1) с прямой ОА; 2) с лучом ОВ?
239. Сколько касательных можно провести к окружности через точку: 1) лежащую на окружности; 2) лежащую внутри окружности; 3) лежащую вне окружности?
240. Через точку А окружности ω (О; r) проведены касательные АВ и АС. Точки В и С — точки касания. Докажите, что АС = АВ.
241. Даны окружности (О; 4 см) и (О; 5 см), ОО1 = 6 см. Имеют ли эти окружности общую точку?
242. Окружности с радиусами 4 и 5 дм касаются друг друга. Найдите расстояние между их центрами, когда они касаются внешне и касаются внутренне.
243. Внутрь прямого угла вписана окружность. Хорда, соединяющая точки касания, равна 40 см. Вычислите расстояние от центра окружности до хорды.
244. Каково взаимное расположение окружностей (О;R) и (О′;R′), если:
1) d = 1 дм, R = 0,8 дм, R′ = 0,2 дм;
2) d = 40 см, R = 110 см, R′ =70 см;
3) d = 12 см, R = 5 см, R′ = 3 см?