Определения
Определение. Окружность, проходящую через вершины треугольника, называют окружностью, описанной около треугольника.
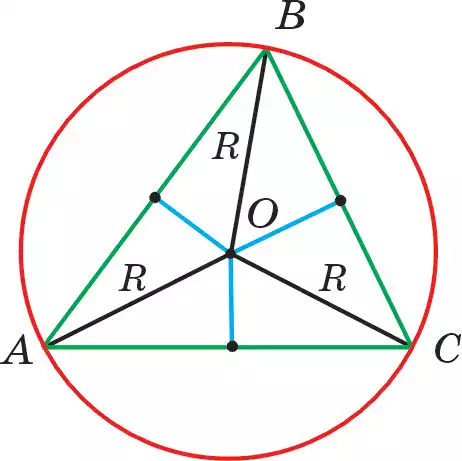
Если точка О будет центром окружности, описанной около треугольника АВС, тогда понятно, что ОА = ОВ = ОС. Значит, центр окружности, описанной около треугольника, лежит на пересечении перпендикуляров, проходящих через середины его сторон, потому что точка О, выполняющая условие ОА = ОВ, лежит на перпендикуляре, проходящем через середину отрезка АВ. То же самое можно сказать и о ОВ = ОС (рис. 103).
Итак, приходим к выводу, что через три точки, не лежащие на одной прямой, можно провести лишь одну окружность.
Определение. Окружность, касающаяся всех сторон треугольника, называется окружностью, вписанной в треугольник.
Касательная окружности перпендикулярна радиусу, проведенному в точку касания. Поэтому, если точка О является центром вписанной в треугольник АВС окружности, тогда отрезки ОМ, ОD, ОЕ равны и перпендикулярны соответственно сторонам треугольника АВ, ВС, СА.
Здесь М, D, Е — точки касания окружности и сторон треугольника. Следовательно, центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника, отрезки ОМ = ОD = ОЕ .
Такая окружность единственная. Потому что центр О и радиус ОМ определяются единственным способом (рис. 104).

Следовательно, для нахождения центра окружности, вписанной в треугольник, нужно провести биссектрисы двух углов треугольника. Их пересечение и будет центром искомой окружности. Из этого центра проводим перпендикуляр к какой-нибудь стороне треугольника. Длину этого перпендикуляра берем за радиус и проводим окружность. Она и будет искомой окружностью.
Вопросы
1. Какие знания были использованы при определении: а) окружности, описанной около треугольника; б) окружности, вписанной в треугольник?
2. В каком случае совпадают центры окружностей: описанной около треугольника и вписанной в треугольник?
Упражнения
245. Дана окружность. Начертите произвольный треугольник, вписанный в эту окружность.
246. Дан треугольник. Постройте прямые, проходящие через середины его сторон и перпендикулярные этим сторонам.
247. Начертите окружность, описанную около треугольника.
248. Докажите, что прямые, проходящие через середины сторон треугольника, перпендикулярные соответствующим сторонам, пересекаются в одной точке.
249. Начертите окружность, описанную около прямоугольного треугольника.
250. Докажите, что высоты треугольника пересекаются в одной точке. Указание. Через каждую вершину данного треугольника проведите
прямую, параллельную противоположной стороне.
251. Дан треугольник. Начертите биссектрисы его углов.
252. Дан треугольник. Начертите окружность, вписанную в этот треугольник.
253. Докажите, что биссектрисы треугольника пересекаются в одной точке.
254. 1) Постройте окружность, вписанную в равносторонний треугольник. 2) Покажите простой способ построения описанной окружности около равностороннего треугольника.
255. Дан ΔАВС. Найдите пересечение биссектрисы ∠А и биссектрис внешних углов — ∠В и ∠С.
256. Постройте треугольник, если даны две его стороны и радиус описанной окружности.
257. Постройте треугольник по его стороне, углу и радиусу вписанной окружности.