Геометрическое построение
А. Понятие о геометрическом построении.
Известно, что при изучении геометрии для построения отдельных фигур применяются специальные инструменты. Так, например, для того чтобы начертить прямую, отрезок и луч, применяется линейка, а для окружности — циркуль. Поэтому геометрические построения можно определить следующим образом: геометрическими построениями называются построения каких-либо геометрических фигур с помощью циркуля и линейки.
Далее, мы геометрические построения рассмотрим на плоскости, поэтому фигуры, данные на построение, и построенные фигуры считаем лежащими на плоскости.
Считается, что геометрические построения теоретически выполняются абсолютно точно. Но на практике они могут быть построены и не точно. Это связано с точностью применяемых инструментов и отдельными недостатками выполнения построений.
Геометрические построения в большинстве случаев даются в виде задач. А потому их можно называть геометрическими задачами на построение.
В условии и требовании таких задач данные фигуры, а также и фигуры, построение которых требуется в задаче, указываются однозначно. Например, в задаче “Постройте окружность, описанную около треугольника” в качестве данной фигуры берется треугольник, а в качестве искомой фигуры — окружность.
Каждая фигура, удовлетворяющая условиям данной геометрической задачи на построение, является решением задачи. Следовательно, под решением геометрической задачи на построение мы понимаем построение фигуры, удовлетворяющей условию этой задачи. Значит, в вышеприведенной задаче ее решением считается окружность.
Требования к решению задач на построение
К решению геометрических задач на построение, как правило, предъявляются определенные требования.
Эти требования принимаются как основные положения теории геометрических построений.
1. Фигуры, данные в задаче, считаются построенными.
Суть этого требования заключается в следующем. Данные в условии задачи фигуры рассматриваются как уже построенные, поэтому их предварительно строят. Например, если в условии задачи будет сказано: “Постройте треугольник по двум сторонам и углу между ними”, то предварительно построим две стороны (отрезки) и угол. Лишь после этого строится искомая фигура. Запись условия геометрической задачи на построение именно этим и отличается от записи условия геометрической задачи на вычисление и на доказательство.
2. Любая точка, лежащая на построенной фигуре, считается построенной.
Действительно, если, например, в условии задачи будет дана какая-то окружность, т. е. будет построена, то на окружности можно отметить любую точку и рассмотреть ее как построенную.
3. Любую точку, не лежащую на построенной фигуре, можно рассмотреть как построенную.
(Это положение объясняется как второй случай.)
Инструменты, применяемые при решении задач на построение
Основными инструментами, применяемыми для решения задач на построение, являются линейка и циркуль.
Построения, выполняемые с помощью любого из них, принимаются как функции этих инструментов.
1. С помощью линейки можно выполнить следующие построения:
а) Строится прямая, проходящая через данные две точки. Существование прямой, проходящей через любые две точки, показывается с помощью известной аксиомы геометрии. Известно построение прямой, проходящей через данные (построенные) две точки. Отрезок и луч являются частями прямой, поэтому их легко построить.
б) Если будут даны две прямые и они пересекаются, то считается, что их точка пересечения тоже построена. Пусть построены данные две прямые. Тогда для построения их сечения нужно с помощью линейки продолжать эти прямые до взаимного пересечения.
2. С помощью циркуля можно выполнить следующие построения:
а) Взяв данную точку за центр и данный отрезок за радиус, можно построить окружность.
б) Если данные две окружности пересекутся, тогда можно построить их точки пересечения. Для этого нужно построить окружности, а лишь после этого определить их точки пересечения.
Таким образом, с помощью циркуля и линейки можно выполнить вышеуказанные основные построения, кроме этого, если пересекаются данная окружность и прямая, то всегда возможно построить их точки пересечения.
Простые задачи на построение
В. Простые задачи на построение.
Решение любой задачи на построение приводит к построению тех или иных точек (например, к построению вершин треугольника), а построение таких точек, в свою очередь, приводит в основном к нахождению пересечения геометрических мест точек (пересечение двух окружностей, пересечение прямой с
окружностью или пересечение двух прямых). Окружность рисуют циркулем, а прямую — линейкой, и значит, задачи на построение также решим с помощью этих инструментов (циркуля и линейки).
Другие инструменты, используемые при решении задач на построение, также имеют особое значение. Например:
1. С помощью транспортира легко можно решить задачу на построение треугольника по двум сторонам и углу между ними в 30°. А если требуется решить эту задачу другим путем, т. е. с помощью циркуля и линейки, тогда ее решение значительно осложняется.
2. Если задача на построение угла в 40° в данной точке прямой легко решается с помощью транспортира, то ее невозможно решить с помощью циркуля и линейки.
Именно в этом мы видим особое значение циркуля и линейки и специально рассматриваем геометрические задачи, решаемые с помощью применения исключительно только этих двух инструментов, так как именно они способствуют развитию ваших конструктивных способностей.
При решении отдельных геометрических сложных задач на построение с помощью циркуля и линейки приходится предварительно решить ряд простых задач, являющихся вспомогательными для решения сложных. Их мы называем простыми геометрическими задачами на построение.
Задача 1
Задача 1. Постройте угол, равный данному углу.
Р е ш е н и е . Пусть дан ∠АОВ (рис. 105).
Требуется построить ∠СDЕ, равный ∠АОВ.
С произвольным радиусом r рисуем дугу ω(О; r), она пересекает стороны данного угла АОВ в точках К и L. Проводим произвольную дугу ω1(D; r) с тем же радиусом. Эта дуга пересекает прямую DС в точке М. На одной из полуплоскостей относительно прямой DС проводим дугу ω2(М; KL). Пересечением этих дуг будет точка N. Проводим луч DN, в результате ∠СDЕ = ∠АОВ. Действительно, по построению ΔKOL = ΔМDN (по трем соответствующим равным
сторонам). Тогда ∠KOL= ∠МDN или ∠АОВ= ∠СDЕ — искомый угол.
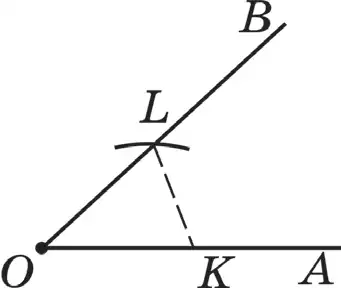
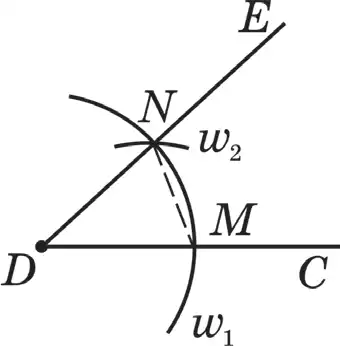
Рисунок 105
Задача 2
Задача 2. Постройте биссектрису данного угла.
Р е ш е н и е . Пусть дан ∠АОВ (рис. 106). Требуется построить его биссектрису ОЕ. Проводим с произвольным радиусом r дугу ω (О; r). Она пересекает стороны данного угла АОВ в точках C и D. Из двух центров в точках С и D с одним и тем же радиусом r проводим две дуги ω1(С; r) и ω2(D; r). Обозначим точку пересечения двух дуг ω1(С; r) и ω2(D; r) с точкой Е (не совпадающей с точкой О). Тогда луч ОЕ и будет искомой биссектрисой. Поскольку
ΔОСЕ =ΔОDЕ (по трем равным сторонам). Откуда получается, что ∠СОЕ = ∠DОЕ или ОЕ есть биссектриса.
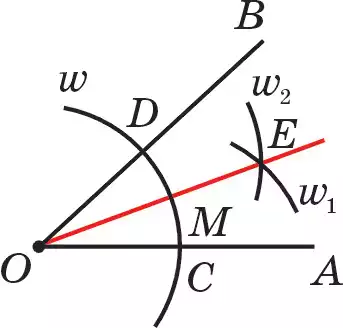
Задача 3
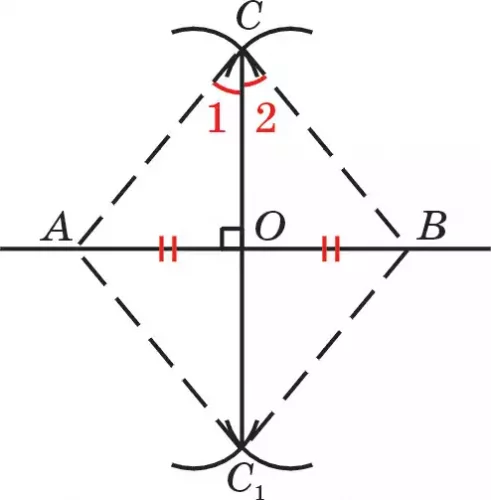
Задача 3. Разделите данный отрезок на две равные части.
Р е ш е н и е . Пусть дан отрезок АВ (рис. 107). Требуется разделить его на две равные части. Прямая АВ делит плоскость на две полуплоскости, если проведем полуокружности ω1(А; АВ) и ω2(В; АВ), то они пересекаются в точках С и С1, которые лежат на разных полуплоскостях. Поэтому отрезок С С1 пересекает прямую АВ в точке О.
Точка О делит отрезок АВ на две равные части. В самом деле, по построению ΔАСС1= ΔВСС1. Тогда ∠1 = ∠2. ΔАСО = ΔВСО (СO — общая сторона, ∠АС = ∠СВ, ∠1 = ∠2). В результате имеем, что АО = ОВ. Значит, точка О делит отрезок АВ на две равные части.
Следствие задачи 3
Следствие. Геометрическое место точек (г.м.т.), лежащих на равном расстоянии от концов отрезка, определяет прямую, проходящую через середину отрезка и перпендикулярную к нему.
Действительно, каждая точка прямой СС1 (рис. 107) равноудалена от точек А и В, и ∠АОС = ∠СОВ = 90°.
Задача 4
Задача 4. Постройте прямую, проходящую через данную точку, перпендикулярную к данной прямой.
Р е ш е н и е . Даны прямая а и точка А. Построим прямую b, проходящую через точку А и перпендикулярную прямой а.
Возможны два случая.
а) Точка А лежит на прямой а (рис. 108). На прямой а обозначим также точки С и D, которые должны лежать на разных сторонах от А и быть СА = АD. Проведем две дуги ω(C; r) и ω1(D; r) с радиусом r, большим чем СА, находим их точку пересечения В. На основании следствия задачи 3 прямая ВА является перпендикулярной прямой а, значит, ВА есть искомая прямая b.
б) Точка А лежит вне прямой а (рис. 97). Проводим произвольную дугу (А; r) такую, чтобы она пересекала прямую в двух точках (Е и F). Находим пересечение двух дуг ω1(Е; r) и ω2(F; r), лежащих на той полуплоскости относительно прямой а, где не лежит точка А. Пусть В является такой точкой пересечения. На основании следствия задачи 3 имеем, что А ⊥ В или b ⊥ а. Значит, b является искомой прямой.


Задача 5

Задача 5. Постройте прямую, параллельную данной прямой, проходящую через точку, не лежащую на этой прямой.
Р е ш е н и е . Пусть даны прямая а и точка М, не лежащая на этой прямой (рис. 110). Надо провести прямую b такую, чтобы она проходила через точку М, и была а || b. На основании основного свойства V или на основании аксиомы параллельности прямых можно считать, что
такая прямая будет единственной. Ее можно построить на основании признаков параллельности прямых. Для этого через точку М проводим произвольную прямую l. Она пересекает прямую а в точке В. Если через точку М проведем такую прямую, которая с прямой l
составила бы∠4 =∠3 или ∠1 = ∠2, тогда окажется, что искомая прямая построена. Такое построение рассмотрено в задаче 1.
Построение касательной к окружности
С. Построение касательной к окружности.
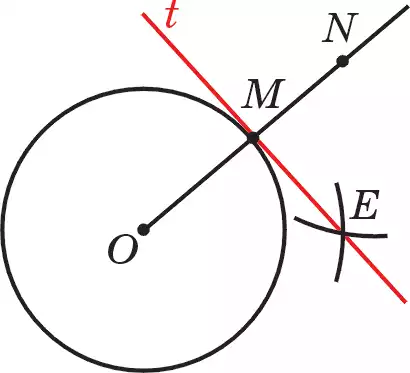
Дана окружность ω(О ; R). Рассмотрим построение касательной к окружности, проведенной в точке М.
Возможны два случая.
а) Точка М лежит на окружности (рис. 111). Пусть t есть искомая касательная. Тогда ОМ ⊥ t. Чтобы построить такую касательную t на продолжении ОМ,
построив ОМ = МN, рисуем дуги ω1(О; r) и ω2(N; r). Здесь r берем таким, чтобы r> R. Точку пересечения дуг обозначим точкой Е. Прямая МЕ, т. е. t будет искомой касательной.
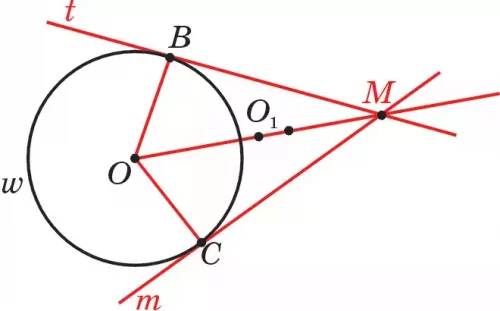
б) Точка М лежит вне окружности (рис. 112). Пусть t есть касательная, проведенная из точки М. В есть точка касания. Тогда ОВ ⊥ t.
Чтобы найти точку касания В, построим прямоугольный треугольник ОМВ. Находим точку О такую, чтобы ОО1= О1М и рисуем окружность ω1(О1;О1М). Эта окружность пересекается с окружностью (О; r) в точках В и С. Прямые МВ и МС, т. е. прямые t и m, будут касательными. Следовательно, из точки вне окружности можно провести к ней две касательные.
Вопросы
1. Чем отличаются задачи на построение от других задач?
2. Какую связь вы видите между этапами решения задач на построение?
Упражнения
258. Даны точки А и В. Постройте: 1) отрезок АВ; 2) луч АВ; 3) прямую АВ.
259. Постройте пересечение прямых а и b.
260. Даны точка О и отрезок а. Постройте окружность с центром О и радиусом а.
261. Дана окружность с центром О и радиусом r. Постройте пересечение прямой, проходящей через точку О и окружности.
262. Даны отрезки а и b. На прямой постройте: 1) сумму этих отрезков; 2) разность этих отрезков.
263. Дан отрезок а. Постройте отрезок, длина которого в три раза больше отрезка а.
264. На прямой даны отрезки АВ = а, ВС = b (а > b). Постройте точки пересечения окружностей (А; а) и (В; b).
265. Даны точка О и отрезок а. Какой фигурой является геометрическое место точек (множества), лежащих от точки О на расстоянии а? Сделайте чертеж.
266. Дан отрезок АВ. Определите и постройте геометрическое место точек (г.м.т.), равноудаленных от точек А и В.
267. Определите и постройте геометрическое место точек (г.м.т.), равноудаленных от сторон угла.
268. Дан треугольник АВС и точка D, лежащая внутри него. Постройте точку, лежащую на одинаковых расстояниях от сторон угла и на расстоянии а от точки D.
269. Докажите, что геометрическим местом точек (г.м.т.), лежащих на расстоянии d от данной прямой, будут две прямые, параллельные а.
270. Найдите и постройте геометрическое место точек (г.м.т.), лежащих на одинаковом расстоянии: 1) от пересекающихся двух прямых; 2) от параллельных двух прямых.
271. Дан треугольник АВС. Постройте точку, лежащую на биссектрисе угла С на одинаковом расстоянии от вершин А и В.
272. Постройте биссектрисы смежных углов.
273. Разделите данный угол на четыре равные части.
274. Постройте угол, который в три раза больше данного.
275. Разделите данную дугу окружности на две равные части.
276. Даны прямая а и точка М, не принадлежащая этой прямой. Постройте прямую, проходящую через точку М и: 1) параллельную, 2) перпендикулярную прямой а.
277. Найдите точку: 1) лежащую на одном и том же расстоянии от трех вершин треугольника;
2) лежащую на одном и том же расстоянии от прямой, пересекающей стороны угла, и от сторон данного угла; 3) равноудаленную от трех сторон треугольника.
278. Дана окружность. Постройте взаимно перпендикулярные диаметры АВ и СD.
279. Даны окружность и ее диаметр. Постройте: 1) хорду АС, которая составляет с данным диаметром угол 45°; 2) хорду АD, которая составляет с этим диаметром угол 60°.
280. Постройте окружность данного радиуса, которая касается стороны данного угла.
281. Какую фигуру представляет геометрическое место центров окружностей, касающихся двух параллельных прямых? Постройте эту фигуру.
282. Какую фигуру образует геометрическое место центров окружностей, касающихся данной прямой? Постройте ее.
283. Найдите геометрическое место центров окружностей, касающихся стороны данного угла. Постройте его.
284. Даны две окружности, не имеющие общие центры и не лежащие одна внутри другой. Постройте их общую касательную.
285. Постройте общую касательную двух касающихся окружностей.