Анализ
При решении сложных задач на построение рекомендуется рассмотреть следующие четыре этапа.
Анализ. Это основной этап решения задач на построение, потому что здесь разрабатывается подробный план выполнения построения. Здесь же указывается связь между элементами, данными в задаче, и элементами, подлежащими построению, определяются пути выполнения и их последовательность.
При проведении анализа, исходя из того, что искомая фигура построена, сделаем приблизительный чертеж, отвечающий условиям задачи. Затем на этом чертеже указываем данные и искомые элементы, и взаимосвязи между ними. Определяем ответ на вопрос: как по данным элементам нужно построить искомые элементы? Именно поэтому анализ называют ключом решения задачи на построение.
Построение
Построение. Этот этап начинается с построения данных элементов искомой фигуры. Далее искомая фигура строится с помощью циркуля и линейки по плану, намеченному при анализе. Следовательно, на данном этапе строится новый чертеж, отличный от чертежа, сделанного при анализе.
Доказательство
Доказательство. Оно проводится для того, чтобы ответить на вопросы, что построенная фигура является действительно искомой, она удовлетворяет всем условиям данной задачи.
Исследование
Исследование. На этом этапе выясняется, имеют ли место в задаче какие-то особые случаи, упрощающие или усложняющие построение.
Задача 1
Задача 1. Постройте треугольник по его стороне, медиане, проведенной к другой стороне, и углу между медианой и данной стороной.
Это первая более сложная задача на построение, поэтому рассмотрим ее решение подробно.
Р е ш е н и е . Дано: сторона (отрезок) а, медиана mb (отрезок), угол α (рис. 113).
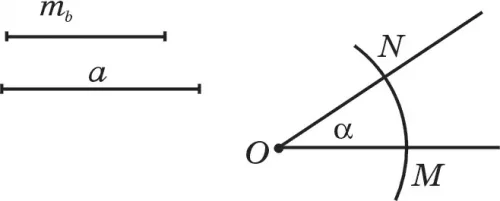
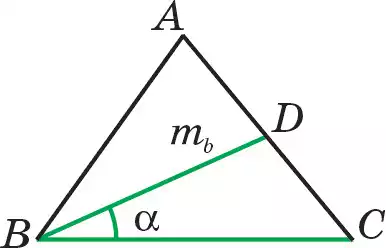
Анализ. Считаем, что искомый треугольник построен. Пусть АВС — искомый треугольник (рис. 114). ВС= а, точка D есть середина стороны АС, ВD =mb, ∠СВD = α.
Чтобы построить треугольник, достаточно построить три его вершины. Здесь вершины В и С легко можно построить. Для этого берем любую прямую l и на ней обозначим точку В. Затем с помощью циркуля отмеряем отрезок а так, чтобы ВС = а, и построим вершину С. Теперь, чтобы построить вершину А, используем остальные условия задачи. Легко можем построить треугольник ВDС, поскольку известны две его стороны и угол между ними. Затем, продолжив сторону СD, отмерив на ней отрезок DА=СD, можно построить вершину А. Таким образом, найдем путь построения задачи.
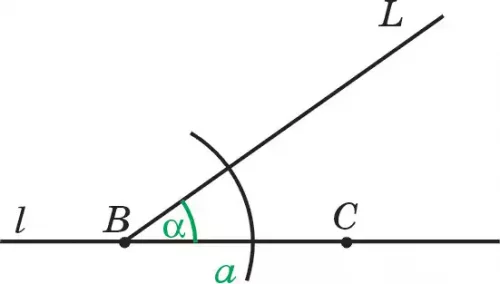
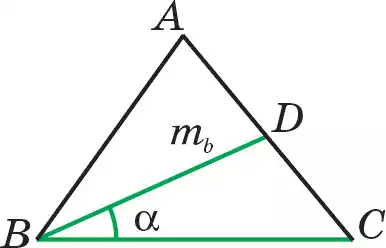
Построение. Проводим прямую l и на ней отмечаем произвольную точку В (рис. 115.1).
Построение выполняется по данным из рис. 114. На прямой l с помощью циркуля, начиная от
точки В, отмерим и отложим отрезок а, строим точку С(ВС=а). Теперь строим угол так, чтобы было выполнено условие ∠СВD = α. Для этого через (О; ОМ) (см. рис. 93) проводим произвольную дугу MN (см. задачу 1). После этого проводятся дуги ω1(D; ОМ) и ω2(Е; МN). В результате получим ∠СВL=α. Затем на луче, построив медиану ВD=mb (она дана), находим
точку D. Теперь, отложив на луче СD, начиная от точки D, отрезок DА=СD, находим точку А. Если соединим точки А, В, С отрезками, то получим искомый треугольник АВС (рис. 115.2).
Доказательство. Доказательство всегда проводится относительно рисунка, выполненного при построении (рис.115.2). Построенный треугольник АВС удовлетворяет условию задачи, потому что по построению ВС = а, ∠СВD = α, ВD =mb. А также, поскольку СD = DА, то ВD = mb — будет медианой. Значит, треугольник АВС со всеми элементами полностью удовлетворяет условию задачи.
Исследование. Задача имеет решение при любой длине стороны а и медианы mb. Но она имеет решение только тогда, когда угол удовлетворяет условию 0< α <180°. В этом случае мы всегда можем построить треугольник ВСD, а значит, и треугольник АВС. Однако при α больше или равно 180° задача не имеет решений. Так как сумма внутренних углов треугольника равна 180°, то один его угол, а также угол между медианой и стороной, исходящих из одной вершины, должен быть всегда меньше 180°.
Итак, задача имеет только одно решение, потому что величины, данные в условии задачи, можно построить только одним способом. Безусловно, при решении легких (простых) задач нет необходимости проводить все эти четыре этапа.
Задача 2
Задача 2. Постройте треугольник, если даны две стороны и угол, лежащий против меньшей из этих сторон. Остановимся подробно на решении этой задачи.
Анализ. Для того чтобы составить план решения задачи, предположим, что она решена, т. е. пусть даны стороны АВ и ВС (ВС<АВ) и ∠А (рис.116). В этих условиях, чтобы построить треугольник АВС, нужно сначала построить угол, равный ∠А, и на одной стороне этого угла, начиная с вершины, отмерить и отложить большую сторону. Получаем две вершины (А и В) треугольника, что четко видно на рисунке. Чтобы найти третью вершину С треугольника, проводим дугу с центром в точке В и радиусом, равным меньшей стороне. Третья вершина С треугольника находится на пересечении этой дуги с другой стороной угла.


Рисунок 116
Построение. Построив угол, равный данному углу, на одной его стороне, начиная от вершины, отмерим и отложим большую сторону из данных двух сторон. Из конца (не лежащего на вершине угла) длинной стороны как из центра, проводим окружность с радиусом, равным меньшей стороне. Эта окружность, пересекаясь с другой стороной угла, дает нам третью вершину треугольника.
Доказательство. Полученный из вышеизложенного построения треугольник является искомым треугольником, поскольку этот треугольник удовлетворяет всем условиям задачи. В самом деле, ∠А был построен как равный данному углу. Сторона АВ была построена равной большей стороне, сторона ВС была построена равной меньшей стороне, угол А был размещен напротив меньшей стороны из двух данных.
Исследование. Сколько решений может иметь эта задача? Может ли она иметь только одно решение при всех значениях данных? Или она может иметь еще другие решения?
Поскольку данный угол лежит против меньшей стороны, то он всегда обязательно должен быть меньше прямого угла, в противном случае угол, лежащий против большей стороны, был бы еще большим (следовательно, сумма только двух углов треугольника была бы больше 180°), чего быть не должно.
Итак, в зависимости от различных значений данного острого угла задача может иметь или одно решение (в этом случае искомым треугольником будет прямоугольный треугольник, при этом окружность с центром в точке В и радиусом, равным ВС, с прямой АС касается только в одной точке М), или два решения (в этом случае один из искомых треугольников будет тупоугольным, а второй будет остроугольным и здесь окружность с центром в точке В и радиусом ВС прямую АС пересекает в двух точках) или не может иметь ни одного решения (в этом случае окружность с центром в точке В и радиусом
ВС не пересекается с прямой АС и не касается с ней. Все это видно на рис. 117).
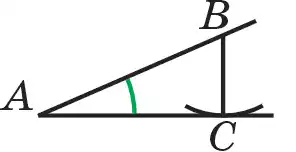
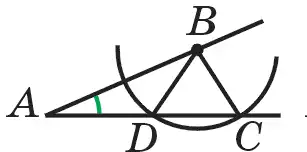
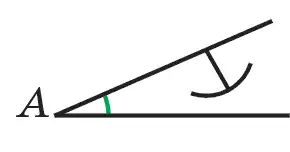
Рисунок 117
Упражнения
286. Дана прямая l и точка М, лежащая вне прямой. Найдите точку на прямой l, лежащую от точки М на расстоянии а. Проведите исследование в зависимости от значения а.
287. Даны прямая а и точка М вне этой прямой. Постройте прямую, проходящую через точку М и: 1) параллельную; 2) перпендикулярную данной прямой.
288. Постройте равнобедренный треугольник по: 1) боковой стороне и углу при вершине; 2) боковой стороне и углу при основании; 3) основанию и высоте, опущенной к нему.
289. Постройте прямоугольный треугольник по: 1) катетам и гипотенузе; 2) катету и острому углу; 3) гипотенузе и острому углу.
290. Постройте треугольник по: 1) двум сторонам и медиане, проведенной к одной из них; 2) двум сторонам и высоте, опущенной к одной из них.
291. Какой фигурой является геометрическое место центров окружностей, касающихся двух параллельных прямых? Постройте эту фигуру.
292. Какой фигурой является геометрическое место центров окружностей, касающихся данной прямой? Постройте эту фигуру.
293. Постройте геометрическое место центров окружностей, касающихся сторон данного угла.